XV. Manipulation de types abstraits de données▲
XV-A. Introduction▲
Si vous avez pratiqué un tant soit peu la programmation par vous-même en dehors de
ce guide, vous vous êtes certainement rendu compte que dés qu'un programme doit
manipuler des données un peu volumineuses ou structurées, il se pose le problème
souvent épineux de la représentation de ces données à l'intérieur du programme.
Pourquoi un tel problème ? Parce que la plupart des langages, Pascal Objet entre
autres, ne proposent que des types "simples" de données (mêmes les tableaux et les
enregistrements seuls suffisent rarement à tout faire).
La plupart des programmes que vous serez amenés à écrire nécessiteront l'emploi de
structures de données plus complexes que celles proposées par Pascal Objet, seules
capables de manipuler par exemple des données relatives à une file d'attente ou des
données hiérarchisées. La création de types de données évolués et efficaces pose
souvent de gros problèmes aux débutants, d'où ce chapitre présentant ces types,
appelés ici "Types abstraits de données", ou TAD. Ils sont introduits (pour ceux
d'entre vous qui ne les connaissent pas), puis implémentés à partir des possibilités
offertes par le langage Pascal Objet (ceci est possible dans beaucoup d'autres
langages). Ils permettent de modèliser à peu près n'importe quel ensemble de données
soi-même. En contrepartie de leur puissance, l'emploi de ces structures complexes
est souvent malaisé et nécessite une attention et une rigueur exemplaire.
Delphi propose des classes toutes faites permettant de manipuler des TAD simples
comme les "piles", les "files" et les "listes" (classes TStack, TFile et TList),
mais le but de ce chapitre n'est en aucun cas de vous apprendre à vous servir de ces
classes en vous laissant tout ignorer de leur fonctionnement : au contraire, ce
chapitre parlera des notions théoriques (sans toutefois vous noyer dans la théorie)
et nous écrirons ensemble des unités complètes servant à la manipulation de ces
types élaborés. Libre à vous ensuite d'utiliser ces classes qui ne sont pas si mal
faites que ça. Le langage Pascal Objet préconise d'ailleurs l'utilisation d'objets
plutôt que de procédures/fonctions classiques. Nous aurons l'occasion de créer une
classe à partir d'une de ces structures (l'arbre général) dans les prochains
chapitres, ce qui procurera une bien meilleure méthode d'implémentation (si ce terme
vous laisse froid(e), sachez qu'il signifie à peu près "traduction d'un ensemble
d'idées ou d'un schémas de fonctionnement ou de raisonnement dans un langage de
programmation, ce qui ne devrait pas être beaucoup mieux, désolé...).
Ce chapitre se propose de vous familiariser avec les plus simples des types
abstraits de données que vous aurez à manipuler : "piles", "files", "listes" et
"arbres" (juste un aperçu pour ces derniers). En parallèle de l'étude générale puis
spécifique au language Pascal Objet de ces TAD, des notions plus globales seront
étudiées, comme le tri dans une liste de données. Plusieurs méthodes de tri seront
ainsi abordées parmi lesquelles les célèbres (ou pas...) Tri à Bulles, Tri Shell et
Tri Rapide ("QuickSort" pour les intimes). Enfin, avant de vous lancer dans la
lecture de ce qui suit, assurez-vous de bien avoir lu et compris le chapitre 11 sur
les pointeurs car les pointeurs vont être largement employés ici et dans tous les
sens car ils permettent une implémentation de presque tous les TAD vus ici.
N'ayons pas peur des mots : les notions abordées dans ce chapitre sont nettement
moins faciles à assimiler que celles des chapitres précédents mais sont néanmoins
des plus importantes. J'insiste assez peu sur la théorie et me focalisant sur des
exemples concrets d'implémentation en Pascal Objet. Un mini-projet très connu
attend les plus téméraires à la fin de ce chapitre. Temporairement, je ne
donnerai pas la solution, et je vous laisserai patauger un peu. Si vous avez des
questions, utilisez exclusivement la mailing-list (je
répondrais aux questions si d'autres ne le font pas avant moi). Cette expérience
vous sera d'ailleurs utile pour apprendre à formuler vos questions et à
travailler, dans une certaine mesure, en commun. Si vous avez réalisé le
mini-projet et souhaitez être corrigé, envoyez-le moi si
possible zippé (SANS le fichier .EXE, mon modem 56K vous en remercie d'avance !).
N'envoyez pas de fichier source ni exécutable attaché sur la liste de diffusion, ce
serait inutile car elle est configurée pour les refuser.
Une dernière remarque avant de commencer (j'ai encore raconté ma vie dans cette
intro !) : Certains d'entre vous vont sans aucun doute se demander avant la fin de
ce chapitre, voire dés maintenant, ce qui est plus génant encore, pourquoi je
m'ennuie à vous parler de tout cela alors qu'on peut tout faire avec des bases de
données. Ma réponse est double :
- l'exécution d'un programme faisant appel à une base de données est beaucoup plus lente que celle d'un programme classique, car l'accès aux bases de données nécessite souvent des temps d'attente qui se ressentent pendant l'exécution, à encore plus forte raison si la ou les bases accédée(s) n'est (ne sont) pas locale(s). De plus, la distribution de tels programme nécessite la distribution d'applications externes dont on peut se passer dans les cas les plus simples.
- La notion des structures avancées faisant intensivement appel aux pointeurs et aux techniques de programmation introduites ici est indispensable à tout programmeur digne de ce nom. En effet, ce sont des procédés auquels un programmeur aura rapidemnt affaire dans d'autres langages comme le C, très couramment employé.
XV-B. Piles▲
XV-B-1. Présentation▲
Les "piles", que nous désignerons plutôt par « TAD Pile », permettent de gèrer un
ensemble d'éléments de même type de base, avec comme principe de fonctionnement «
premier dedans, dernier dehors ». Ce type de fonctionnement est très pratique pour
modèliser au niveau du stockage des données des phénomènes existants.
Un exemple parlant est une de ces boites cylindriques dans lesquelles on met les
balles de tennis : lorsque vous voulez une balle, vous n'avez directement
accès qu'à la première balle. Si vous voulez la deuxième, il vous faudra d'abord
enlever la première, puis la deuxième, et ensuite éventuellement remettre la
première. Un autre exemple plus classique mais moins parlant est la pile
d'assiettes. Lorsque vous voulez une assiette, vous prennez celle du dessus, sans
allez prendre la troisième en partant du haut. Pour constituer une telle pile, vous
mettez une assiette n°1, puis une assiette n°2, et ainsi de suite. Lorsque vous
récupèrez les deux assiettes, vous devrez d'abord prendre l'assiette n°2 et ensuite
l'assiette n°1. Un troisième exemple serait un tube de comprimés (de la vitamine C
UPSA par exemple, pour ne pas faire de publicité) par exemple : lorsque vous ouvrez
le tube, vous ne voyez que le premier comprimé, que vous êtes obligé de prendre
pour avoir accès au second. Lorsque ce tube a été rempli, un comprimé n°1 a été
disposé au fond du tube, puis un comprimé n°2, puis... jusqu'au comprimé n°10.
Quoi que vous fassiez, à moins de tricher en découpant le tube, vous DEVREZ
prendre le comprimé n°10, puis le n°9 ... puis le n°1 pour constater que le tube
est vide, comme avant que le fabriquant ne le remplisse.
La suite du paragraphe va certainement vous paraître ennuyeuse, voire saoulante,
mais c'est un passage incontournable avant de passer à la pratique. Essayez de lire
toute la théorie sans vous endormir, puis essayez les exemples, puis enfin revenez
sur la théorie : vous la découvrirez alors sous un jour différent, nettement moins
antipathique.
XV-B-2. Une définition plus formelle▲
Sans pousser le vice jusqu'à vous servir les spécifications du TAD Pile comme je
les ai apprises en Licence Informatique (je ne suis pas méchant à ce point), ce
paragraphe se propose de donner une définition plus formelle des piles. En effet,
on ne peut pas faire tout et n'importe quoi à propos des piles, pour au moins une
(simple) raison : ce sont des piles d'éléments, mais de quel type sont ces éléments
? Comme nous n'avons aucun droit ni moyen de répondre à cette question, il va
falloir en faire abstraction, ce qui est, je vous l'assure, tout-à-fait possible
mais exige une certaine rigueur.
Une pile peut être manipulée au moyen d'opérations de base. Ces opérations sont les
suivantes (pour chaque opération, une liste des paramètres avec leur type et un
éventuel résultat avec son type est indiqué. Ceci devra être respecté dans la
mesure du possible) :
- Création d'une nouvelle pile vide
paramètres : (aucun)
résultat : pile vide - Destruction d'une pile
paramètres : une pile
résultat : (aucun) - Empilement d'un élément (sur le sommet de la pile)
paramètres : une pile et un élément du type stocké par la pile
paramètres : une pile et un élément du type stocké par la pile
résultat : une pile remplaçant complètement celle donnée en paramètre (l'élément a été empilé si possible) - Dépilement d'un élément (retrait du sommet, sous réserve qu'il existe)
paramètres : une pile
résultat : une pile remplaçant complètement celle donnée en paramètre (l'élément a été dépilé si possible) - Test de pile vide qui indiquera si la pile est vide ou non
paramètres : une pile
résultat : un booléen (vrai si la pile est vide) - Test de pile pleine, qui indiquera si la capacité de la pile est atteinte et qu'aucun nouvel élément ne peut être ajouté (cette opération n'est pas toujours définie, nous verrons pourquoi dans les exemples).
paramètres : une pile
résultat : un booléen (vrai si la pile est pleine) - Accès au sommet de la pile (sous réserve qu'il existe)
paramètres : une pile
résultat : un élément du type stocké par la pile
Bien que cela paraisse rudimentaire, ce sont les seules opérations que nous
pourrons effectuer sur des piles. Pour utiliser une pile, il faudra d'abord la
créer, puis autant de fois qu'on le désire : empiler, dépiler, accéder au sommet,
tester si la pile est vide ou pleine. Enfin, il faudra penser à la détruire. Cela
devrait vous rappeler, bien que ce soit un peu hors propos, le fonctionnement des
objets : on commence par créer un objet, puis on l'utilise et enfin on le détruit.
Tout comme les objets, considérés comme des entités dont on ne connait pas le
fonctionnement interne depuis l'extérieur, les piles devront être considérées
depuis l'extérieur comme des boites noires manipulables uniquement avec les
opérations citées ci-dessus.
Au niveau abstrait, c'est à peu près tut ce qu'il vous faut savoir. Cette théorie
est valable quel que soit le language que vous serez amené(e) à manipuler. Nous
allons maintenant voir l'application concrète de cette théorie au seul language qui
nous intéresse ici : le Pascal. Deux manières d'implémenter (de créer une structure
et des fonctions/procédures pratique à manipuler) des piles vont être étudiées : en
utilisant un tableau, et en utilisant des pointeurs. Place à la pratique.
XV-B-3. Implémentation d'une pile avec un tableau▲
Un moyen simple d'implémenter une pile et d'utiliser un tableau. chaque élément de la pile sera stocké dans une case du tableau. Une telle structure ne sera pas suffisante : rien ne permettrait de retrouver facilement le sommet ni de déterminer si la pile est vide ou pleine. Pour ces raisons, nous allons utiliser une valeur entière qui indiquera le numéro de la case qui contient le sommet de la pile, ou -1 par exemple si la pile est vide. Pour rassembler les deux éléments, nous créerons un enregistrement. Enfin, une constante va nous permettre de définir la taille du tableau et ainsi de savoir lorsque la pile sera pleine. Dans nos exemples, nous allons manipuler des chaînes de caractères. Voici les déclarations dont nous auront besoin :
const
TAILLE_MAX_PILE = 300;
type
TPileTab = record
Elem: array[1..TAILLE_MAX_PILE] of string;
Sommet: Integer;
end;
Comme vous pouvez le constater dans le code ci-dessus, un enregistrement de type
TFileTab permettra de manipuler une pile. Les éléments (des chaînes, dans le cas
présent) seront stockés dans le tableau Elem qui peut contenir TAILLE_MAX_PILE
éléments. La position du sommet sera mémorisée dans Sommet. Une valeur de -1
signifiera une pile vide et MAX_TAILLE_PILE une pile pleine (dans laquelle on ne
pourra plus rajouter d'éléments puisque toutes les cases seront remplies). Mais
attention, il va falloir travailler à deux niveaux : le niveau intérieur, où ces
détails ont une signification, et le niveau extérieur où n'existera que le type
TPileTab et les opérations de création, empilement, dépilement, accès au sommet,
test de pile vide ou pleine et destruction. A ce second niveau, TPileTab devra être
considéré comme une boite noire dont on ne connait pas le contenu : ce n'est plus
un enregistrement, mais une pile.
Il va maintenant falloir nous atteler à créer chacune des opérations servant à
manipuler une pile. Chacune de ces opérations va être créée au moyen d'une
procédure ou d'une fonction. Depuis l'extérieur, il nous suffira ensuite d'appeler
ces procédures et ces fonctions pour faire fonctionner notre pile. Ensuite, si nous
devions modifier la structure TPileTab, il faudrait juste réécrire les opérations
de manipulation et si cela a été bien fait, aucune des lignes de code utilisant la
pile n'aura besoin d'être modifiée.
Note 1 : sous Delphi, il est possible pour une fonction de retourner un type enregistrement. Nous nous servons de cette possibilité assez rare pour simplifier les choses. Cependant, la plupart des languages ne permettent pas de retourner un enregistrement, c'est pourquoi il faudra alors impérativement passer par des pointeurs comme nous le ferons dans la deuxième implémentation.
Note 1 : certaines opérations comme Empiler, Dépiler et Sommet devront être utilisées avec précaution. Ainsi, il faudra systématiquement tester que la pile n'est pas pleine avant d'empiler, même si ce test sera à nouveau réalisé lors de l'empilement. Il faudra également toujours tester que la pile n'est pas vide avant de dépiler ou d'accèder au sommet de la pile. Voici tout de suite le code source de PTNouvelle qui crée une nouvelle pile vide.
function PTNouvelle: TPileTab;
begin
result.Sommet := -1;
end;Le code ci-dessus ne devrait pas poser de problème : on retourne un enregistrement de type TPileTab dans lequel on fixe le sommet à -1, ce qui dénote bien une pile vide. Passons tout de suite aux indicateurs de pile vide ou pleine :
function PTVide(Pile: TPileTab): Boolean;
begin
result := Pile.Sommet = -1;
end;
function PTPleine(Pile: TPileTab): Boolean;
begin
result := Pile.Sommet = TAILLE_MAX_PILE;
end;La fonction PTVide compare la valeur du champ Sommet de la pile transmise à -1, et si le résultat est vrai, alors la pile est vide et on retourne True, sinon, on retourne False. Nous aurions pû écrire un bloc if faisant la comparaison et retournant True ou False selon les cas, mais il est plus rapide de constater que la valeur de Result est la valeur booléenne renvoyée par la comparaison Pile.Sommet = -1, d'où l'affectation directe qui peut dérouter au début mais à laquelle il faudra vous habituer. PTPleine marche suivant le même principe mais compare la valeur de Sommet à TAILLE_MAX_PILE : si les valeurs correspondent, la pile est pleine et le résultat renvoyé est True, sinon False, d'où encore une fois l'affectation directe qui évite d'écrire inutilement un bloc if. Passons maintenant à un morceau de choix : l'empilement.
function PTEmpiler(Pile: TPileTab; S: string): TPileTab;
begin
result := Pile;
if not PTPleine(result) then
begin
if result.Sommet = -1 then
result.Sommet := 1
else
inc(result.Sommet);
result.Elem[result.Sommet] := S;
end;
end;L'empilement se doit de fournir une nouvelle pile contenant si cela est possible l'élément à empiler. Dans notre cas, cela paraît un peu farfelu, mais lorsque nous parlerons de pointeurs, vous verrez mieux l'intérêt de la chose. Le résultat est d'abord fixé à la valeur de la pile transmise, puis si la pile n'est pas pleine (s'il reste de la place pour le nouvel élément), ce résultat est modifié. En premier lieu, le sommet est incrémenté, ce qui permet de le fixer à la position du nouveau sommet. Ce nouveau sommet est fixé dans l'instruction suivante. La pile ainsi modifiée est retournée en tant que résultat. Voyons maintenant le dépilement :
function PTDepiler(Pile: TPileTab): TPileTab;
begin
result := Pile;
if not PTVide(result) then
begin
result.Elem[result.Sommet] := '';
if result.Sommet > 1 then
dec(result.Sommet)
else
result.Sommet := -1;
end;
end;
PTDepiler fonctionne sur le même principe que la fonction précédente : le résultat
est d'abord fixé à la pile transmise, puis modifié cette fois si la pile n'est pas
vide (s'il y a un élément à dépiler). A l'intérieur du bloc if testant si la pile
n'est pas vide, on doit mettre à jour la pile. On commence par fixer la chaîne
indexée par Sommet à la chaîne vide (car cela permet de libérer de la mémoire,
faites comme si vous en étiez convaincu(e) même si ça ne paraît pas évident,
j'expliquerai à l'occasion pourquoi mais ce n'est vraiment pas le moment), puis la
valeur de Sommet est soit décrémentée, soit fixée à -1 si elle valait 1 avant (car
alors le dépilement rend la pile vide puisqu'il n'y avait qu'un élément avant de
dépiler).
Après ces deux fonctions un peu difficiles, voici la procédure qui détruit une pile
: dans le cas particulier de notre structure utilisant un enregistrement, nous
n'avons rien à faire, mais la procédure ci-dessous a un but purement éducatif :
elle vous-montre comment il faut normalement détruire une pile.
procedure PTDetruire(Pile: TPileTab);
var
P: TPileTab;
begin
P := Pile;
while not PTVide(P) do
P := PTDepiler(P);
end;Le fonctionnement est le suivant : on dépile jusqu'à ce que la pile soit vide. Ensuite, il suffit de supprimer la pile vide, ce qui dans notre cas se résume à ne rien faire, mais ce ne sera pas toujours le cas. Voici enfin la fonction qui permet d'accèder à l'élément au sommet de la pile. Notez que cette fonction ne devra être appelée qu'après un test de pile vide, car le résultat n'a aucune signification si la pile est vide !
function PTSommet(Pile: TPileTab): string;
begin
if PTVide(Pile) then
result := ''
else
result := Pile.Elem[Pile.Sommet];
end;
La fonction est relativement simple : si la pile est vide, on est bien obligé de
retourner un résultat, et donc on renvoie une chaîne vide. Dans le cas favorable où
la pile n'est pas vide, la chaîne dans la case indexée par Pile.Sommet est
renvoyée, car c'est cette chaîne qui est au sommet de notre pile.
Enfin, il va nous falloir dans la suite de l'exemple une opération permettant de
connaître le contenu de la pile. Cette opération, qui ne fait pas partie des
opérations classiques, est cependant indispensable pour nous afin de montrer ce qui
se passe lorsque les autres opérations sont appliquées. Voici le code source de la
procédure en question :
procedure PTAffiche(Pile: TPileTab; Sortie: TStrings);
var
indx: integer;
begin
Sortie.Clear;
if Pile.Sommet = -1 then
Sortie.Add('(pile vide)')
else
begin
if Pile.Sommet = TAILLE_MAX_PILE then
Sortie.Add('(pile pleine)');
for indx := Pile.Sommet downto 1 do
Sortie.Add(Pile.Elem[indx]);
end;
end;
La procédure ci-dessus accepte deux paramètres : la pile à afficher et la sortie
dans laquelle afficher, de type TStrings. Je vous rappelle que TStrings est le
type de la propriété Lines des composants "Mémo" ainsi que de la propriété Items
des composants "ListBox". Ainsi, nous pourrons utiliser une zone de liste ou un
mémo et transmettre une de leur propriété et l'affichage se fera dans le
composant en utilisant le paramètre objet "Sortie" qui permet de dialoguer avec
le composant sans savoir ce qu'il est exactement. L'intérêt d'utiliser un type
TStrings est justement cela : la procédure qui "affiche" la pile est indépendante
d'un type de composant particulier puisque tout se fait en dialoguant avec un
objet et pas un composant particulier. La première instruction vide la liste des
chaînes. Ensuite, soit la pile est vide et seule une ligne indiquant cet état de
fait est insérée, soit l'affichage des chaînes a lieu. Un test supplémentaire
permet de signaler une pile pleine en insérant un message explicite. Ensuite,
les chaînes sont insérées en commençant par celle qui a le numéro Pile.Sommet,
qui est donc le sommet de pile, jusqu'à celle qui a le n°1.
C'en est assez d'explications dans le vide. Nous allons créer un projet utilisant
tout cela. Vous avez ici trois possibilités :
- Soit vous êtes courageux(se) et vous avez reconstitué une unité avec l'ensemble des sources proposés, dans ce cas ne vous privez pas de l'utiliser.
- Soit vous êtes mi-courageux(se), mi-paresseux(se), et vous pouvez télécharger seulement l'unité toute faite ici :piles_tab.pas et réaliser le projet en suivant les indications ci-dessous.
- Soit vous êtes paresseux(se) et vous pouvez télécharger le projet complet et suivre les indications (ne faites ça que si vous n'avez pas réussi à le faire vous-même) : piles1.zip
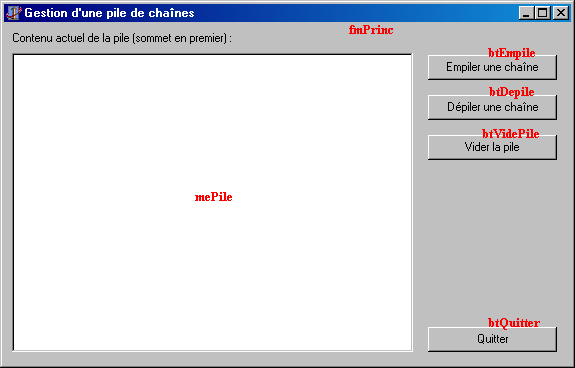
Passons maintenant à la réalisation pratique. Créez un projet et créez une interface ressemblant à celle-ci :
Le but de cette interface va être de démontrer visuellement comment fonctionne une pile et les effets des diverses opérations sur une pile. Déclarez dans l'unité principale une variable "Pile" de type TPileTab (à vous de voir où c'est le plus avantageux). Générez la procédure associée à l'événement OnCreate de la fiche et entrez le code suivant :
procedure TfmPrinc.FormCreate(Sender: TObject);
begin
Pile := PTNouvelle;
end;Cette simple ligne de code nous permet de créer la pile au démarrage de l'application (lors de la création de la fiche principale). L'opération de création renvoie une nouvelle pile vide qui initialise "Pile". Générez de même la procédure associée à OnDestroy et entrez ce qui suit, qui détruit la pile lors de la destruction de la fiche, lorsque l'application se termine :
procedure TfmPrinc.FormDestroy(Sender: TObject);
begin
PTDetruire(Pile);
end;Nous allons maintenant écrire une procédure qui va nous permettre de mettre l'interface de notre petite application à jour en fonction des modifications apportées à la pile. Cette procédure réaffichera la pile et permettra d'activer ou non certains boutons. Voici ce que cela donne :
procedure MajInterface;
var
vide: boolean;
begin
PTAffiche(Pile, fmPrinc.mePile.Lines);
fmPrinc.btEmpile.Enabled := not PTPleine(Pile);
vide := PTVide(Pile);
fmPrinc.btDepile.Enabled := not vide;
fmPrinc.btVidePile.Enabled := not vide;
end;Dans la code ci-dessus, la pile est affichée au moyen de PTAffiche auquel on transmet la pile et la propriété Lines du méoo : ainsi, le méme va se voir ajouter les lignes correspondantes aux divers cas possibles pour la pile par la procédure PTAffiche. Ensuite, les 3 boutons de manipulation de la pile sont (dés)activés. Le premier n'est activé que lorsque la pile n'est pas pleine, alors que les deux derniers ne le sont que lorsqu'elle n'est pas vide. Notez que le test de pile vide n'est effectué qu'une fois et qu'ensuite la valeur booléenne résultante est utilisée, ce qui permet d'économiser du temps en n'appelant qu'une seule fois la fonction PTVide. Reste maintenant à écrire les procédures associées aux 4 boutons. Voici celle associée au bouton "Empiler" :
procedure TfmPrinc.btEmpileClick(Sender: TObject);
var
S: String;
begin
if InputQuery('Empilement d''une chaîne', 'Saisissez une chaîne à empiler', S) then
begin
Pile := PTEmpiler(Pile, S);
MajInterface;
end;
end;Cette procédure demande une chaîne à l'utilisateur à l'aide de la fonction InputQuery. Si l'utilisateur rentre effectivement une chaîne, elle est empilée sur Pile et l'interface est mise à jour : rien de très difficile à comprendre ici. La procédure associée au bouton Dépiler est encore plus simple :
procedure TfmPrinc.btDepileClick(Sender: TObject);
begin
Pile := PTDepiler(Pile);
MajInterface;
end;Lors d'un clic sur le bouton Dépiler, une chaîne est dépilée de Pile, puis l'interface est mise à jour pour reflèter le changement. Passons enfin à la procédure associée au bouton "Vider la pile" qui présente plus d'intérêt :
procedure TfmPrinc.btVidePileClick(Sender: TObject);
begin
while not PTVide(Pile) do
Pile := PTDepiler(Pile);
MajInterface;
end;Cette procédure utilise les opérations standard pour vider la pile : tant qu'on peut dépiler, on le fait, jusqu'à épuisement du stock de chaînes. L'interface est ensuite actualisée. Le projet est a peu près terminé : il ne vous reste plus qu'à programmer le bouton "Quitter" et à lancer l'application : ajoutez des chaînes, retirez-en, et videz. Si vous avez un problème insoluble, téléchargez le projet complet.
XV-B-4. Compléments sur les pointeurs : chaînage et gestion de la mémoire▲
Un sujet importantissime qu'il me faut aborder ici est celui du chaînage. Si vous
êtes un(e) initié(e), vous vous dites sûrement : "enfin !", sinon : "mais de quoi
il parle ???" (et je vais vous faire languir un petit peu). Le chaînage est une
notion née d'un besoin assez simple à comprendre : celui de gèrer dynamiquement la
mémoire disponible pendant l'exécution d'une application. Les deux notions évoquées
dans le titre de ce paragraphe sont donc relativement proches l'une de l'autre
puisque la seconde est une nécessité qu'aucun programmeur sérieux ne saurait
ignorer, et la première est un moyen très conventionnel la facilitant.
Mais assez parlé par énigmes : la gestion de la mémoire disponible est souvent
nécessaire pour de moyennes ou de grosses applications. En effet, il est souvent
impossible de prévoir quelle quantité de mémoire sera nécessaire pour éxécuter une
application, car cela dépend essentiellement de la taille des données manipulées
par cette application. Puisque la quantité de mémoire nécessaire est inconnue, une
(très) bonne solution est d'en allouer (de s'en réserver) au fur et à mesure des
besoins, et de la libérer ensuite. Ainsi, l'application utilisera toujours le
minimum (parfois un très gros minimum) possible de mémoire, évitant ainsi de
s'incruster en monopolisant la moitié de la mémoire comme certaines "usines à gaz"
que je ne citerai pas car mon cours est déjà assez long comme ça.
L'allocation dynamique passe la plupart du temps par l'utilisation de pointeurs.
Ces pointeurs permettent, via l'utilisation de new et de dispose, d'allouer et de
libèrer de la mémoire. Mais voilà : une application a très souvent besoin de
stocker un nombre quelconque d'éléments du même type. Les types abstraits de
données que nous étudions dans ce chapitre constituent alors un très bon moyen de
regrouper ces données suivant le type de relation qui existent entre elles. Mais
alors un problème se pose : si on utilise des tableaux, la taille occupée en
mémoire est fixe (si l'on excepte les artifices des tableaux dynamiques non
présents dans la plupart des languages). Une solution est alors le chaînage, notion
très simple qui est déclinée de plusieurs manières, dont je vais présenter ici la
plus simple, et qui a l'avantage d'être adaptable à tous les languages permettant
l'utilisation de pointeurs.
L'idée de départ est très simple : chaque élément va être chaîné à un autre
élément. Chaque élément va donc en pratique être doté d'un pointeur venant
s'ajouter aux données de l'élément. Ce pointeur pointera vers un autre élément ou
vaudra nil pour indiquer une absence d'élément chaîné. Concrètement, voici un petit
morceau de code Pascal Objet qui illustre cela :
type
PPileElem = ^TPileElem;
TPileElem = record
Elem: string;
Suiv: PPileElem;
end;Observez bien cet extrait de code : un premier type PPileElem est déclaré comme étant un pointeur vers un type TPileElem. Ce type, bien qu'encore non défini, n'est pas nécessaire dans le cas d'un type pointeur (Lisez la note ci-dessous si vous voulez en savoir plus). Il faudra tout de même que l'on déclare le type en question, TPileElem. Ceci est fait juste après : TPileElem est un type enregistrement qui contient deux champs, ce qui fait de PPileElem est un pointeur vers un enregistrement. Le premier champ de TPileElem, très conventionnel, est une chaîne. Le second mérite toute notre attention : c'est un champ de type PPileElem, c'est-à-dire un pointeur. Cette définition de type vous interloque peut-être du fait qu'elle a l'air de se "mordre la queue". Cette construction est cependant autorisée.
Définitions récursives de types
La déclaration présente dans le code source ci-dessus est possible et
autorisée. La raison se trouve dans le fait que c'est le compilateur
qui autorise cela. En effet, il a besoin, lorsque vous définissez un
type, de deux informations, qui peuvent être données en une ou deux
fois. Si mes propos vous paraissent obscurs, repensez à l'extrait de
code :
PPileElem = ^TPileElem;
Cette définition donne une seule des deux informations nécessaires à
la création d'un type : la quantité de mémoire occupée par un élément
de ce type. La seconde information, à savoir la nature exacte du type,
n'est pas nécessaire ici, étant donné qu'on déclare un type pointeur,
dont la taille est toujours de 4 octets. Par conséquent, le compilateur
accepte la déclaration, en exigeant cependant que TPileElem soit défini
par la suite.
Dès lors que cette déclaration est acceptée, le type en question est
utilisable pour construire d'autres types. Ceci est fait tout de suite
après dans la déclaration du type TPileElem, ce qui permet d' « entremèler »
les deux déclarations.
Cette construction étéroclite est dite "simplement chaînée" : chaque élément peut (mais n'est pas obligé de) pointer vers un autre élément, ce qui fait que les éléments sont chaînés entre eux dans un seul sens (d'où le "simplement" ; il existe également des constructions plus complexes dites doublement chaînées qui permettent aux éléments d'être liés dans les deux sens, ou même des chaînages dits circulaires où une boucle est réalisée par le biais de pointeurs). En utilisant ce type de chaînage, il est possible de constituer des listes d'éléments. La méthode est relativement simple : on utilise un seul pointeur de type "PPileElem" par exemple, qui pointe sur un élément de type "TPileElem", qui lui-même pointe sur un autre... jusqu'à ce qu'un d'entre eux ne pointe vers rien (son pointeur vers l'élément suivant vaut nil). Il est ainsi possible, si on conserve soigneusement le pointeur vers le premier élément, de retrouver tous les autres par un parcours de la « chaîne ».
XV-B-5. Implémentation par une liste chaînée▲
Nous allons tout de suite mettre ces connaissances en pratique en implémentant un type Pile en utilisant une liste à simple chaînage. Le principe est ici assez simple, mais je vais bien détailler cette fois-ci puisque c'est peut-être la première fois que vous manipulez une liste chaînée. Le principe va être le suivant : on va utiliser un pointeur de type PPileElem égal à nil pour représenter la pile vide.
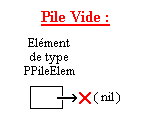
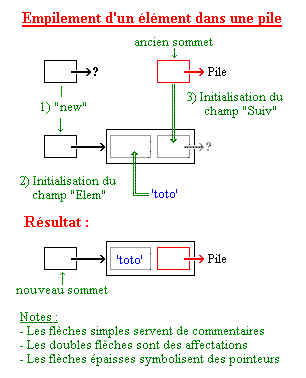
Lors de l'ajout d'un premier élément dans la pile, voici ce que cela donnera :
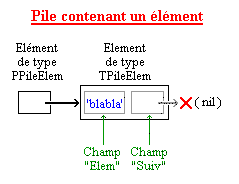
Cela peut paraître contraignant et compliqué, mais ce genre de structure a deux avantages :
- Lorsque la pile est vide, elle ne prend que 4 octets de mémoire, contrairement à un encombrant tableau.
- La taille limite de la pile est la taille mémoire disponible, et non pas une constante fixée arbitrairement au moment du développement de l'application.
Lorsqu'on devra « empiler » un élément, il suffira de créer un nouvel élément par un appel à "new", puis de fixer le champ "Suiv" de cet élément à l'ancien sommet de pile. Le pointeur vers l'élément nouvellement créé devient alors le nouveau sommet de pile. Voici un petit schémas qui illustre cela :
Le dépilement est effectué en inversant les étapes précédentes, à condition
toutefois que la pile ne soit pas vide. La suppression complète se fait en dépilant
jusqu'à vider la pile. Enfin, l'opération de test de pile pleine renverra toujours
faux, car on ne tiendra pas compte ici d'un éventuel remplissage de la mémoire.
Assez de théorie et de beaux schémas, passons au code source.
La fonction PLNouvelle crée une pile vide. Par convention, la pile vide sera un
pointeur nil (rappelez-vous que depuis l'extérieur, la structure véritable cachée
derrière la Pile ne doit pas être considéré comme connu ; le pointeur nil a
donc une signification en "interne", mais pas en "externe"). Voici cette fonction
très simple :
function PLNouvelle: PPileElem;
begin
result := nil;
end;La fonction qui indique si une pile est vide teste simplement si le pointeur transmis est égal à nil.
function PLVide(Pile: PPileElem): Boolean;
begin
result := Pile = nil;
end;La fonction qui permet d'empiler un élément est nettement plus intéressante. Examinez le code source ci-dessous à la lumière du schémas présenté plus haut. Une variable temporaire de type pointeur est déclarée. La première instruction initialise le pointeur en réservant une zone mémoire pointé par celui-ci. Les deux instructions suivantes initialisent l'élément pointé : le champ "Elem" reçoit le nouvel élément, tandis que le champ "Suiv" reçoit l'ancien pointeur vers le sommet de pile (que ce pointeur soit nil ou non importe peu). La quatrième instruction fixe le résultat au pointeur qui vient d'être créé et qui n'est pas détruit ici. C'est là un élément nouveau dans l'utilisation que nous faisons des pointeurs : l'initialisation et la destruction sont séparées ; il faudra donc penser à détruire tous ces pointeurs à un moment donné. Lors de l'appel à "PLEmpiler", la pile actuelle (qui est en fait un pointeur vers le premier élément ou nil) est transmise en paramètre. Le résultat de l'appel à la fonction devra être affecté à ce pointeur pour le fixer à sa nouvelle valeur (l'emplacement du sommet de pile a changé puisque ce sommet a changé).
function PLEmpiler(Pile: PPileElem; S: string): PPileElem;
var
temp: PPileElem;
begin
new(temp);
temp^.Elem := S;
temp^.Suiv := Pile;
result := temp;
end;L'opération de dépilement est sujette à une condition : la pile ne doit pas être vide. Le code de la fonction "PLDepiler" va donc se diviser en deux pour les deux cas : pile vide ou pile non vide. Le second cas est très simple : on ne peut rien dépiler et donc on retourne la pile vide (nil). Le premier cas commence par sauvegarder ce qui sera la nouvelle pile : le champ "Suiv" du sommet de pile, c'est-à-dire nil si la pile ne contenait qu'un seul élément, ou un pointeur vers le second élément de la pile. La seconde étape consiste à libèrer la mémoire associée à l'ancien sommet de pile, en appelant dispose. Notez que l'ordre de ces deux instructions est important car si on détruisait d'abord le pointeur "Pile", on ne pourrait plus accèder à "Pile^.Suiv".
function PLDepiler(Pile: PPileElem): PPileElem;
begin
if Pile <> nil then
begin
Result := Pile^.Suiv;
Dispose(Pile);
end
else
Result := nil;
end;La procédure de destruction d'une pile est assez simple : tant que la pile n'est pas vide, on dépile. Voici le code source qui est presque une traduction litérale de ce qui précède :
procedure PLDetruire(Pile: PPileElem);
begin
while Pile <> nil do
Pile := PLDepiler(Pile);
end;La fonction permettant l'accès au sommet de la pile est également sujette à condition : si la pile est vide, on se doit de retourner un résultat, mais celui-ci sera sans signification. Sinon, il suffit de retourner le champ "Elem" du premier élément de la liste chaînée, à savoir Pile^ .
function PLSommet(Pile: PPileElem): string;
begin
if Pile <> nil then
Result := Pile^.Elem
else
Result := ''; // erreur !!!
end;La dernière procédure qui nous sera utile ici est l'affichage du contenu de la pile. On utilise la même sortie que précédemment : un objet de type TStrings. Le principe est ici de parcourir la pile élément par élément. Pour cela, nous avons besoin d'un pointeur qui pointera sur chacun des éléments de la pile. Ce pointeur est initialisé à la valeur de Pile, ce qui le fait pointer vers le premier élément de la pile. Ensuite, une boucle teste à chaque itération si le pointeur en cours est nil. Si c'est le cas, le parcours est terminé, sinon, on ajoute le champ "Elem" de l'élément pointé et on passe à l'élément suivant en affectant au pointeur la valeur du champ "Suiv", c'est-à-dire un pointeur sur l'élément suivant.
procedure PLAffiche(Pile: PPileElem; Sortie: TStrings);
var
temp: PPileElem;
begin
temp := Pile;
Sortie.Clear;
while temp <> nil do
begin
Sortie.Add(temp^.Elem);
temp := temp^.Suiv;
end;
end;Si vous avez tout suivi, vous avez de quoi reconstituer une unité complète comprenant la déclaration des types et les fonctions et procédures expliquées plus haut. Vous avez ici trois possibilités :
- Soit vous êtes courageux(se) et vous avez reconstitué l'unité par vous-même et vous pouvez continuer.
- Soit vous êtes mi-courageux(se), mi-paresseux(se), et vous pouvez télécharger seulement l'unité toute faite ici : piles_ptr.pas et réaliser le projet ci-dessous en suivant les indications données.
- Soit vous êtes paresseux(se) et vous pouvez télécharger le projet complet et suivre les indications (ne faites ça que si vous n'avez pas réussi à le faire vous-même) : piles2.zip
Afin de gagner du temps et de vous démontrer qu'on peut faire abstraction de la structure réelle des données qu'on manipule, nous allons réécrire le projet précédent en utilisant cette fois une pile gérée par une liste chaînée. Le code source va beaucoup ressembler à celui du projet précédent, je serais donc plus bref dans les explications. Recréez la même interface que précédemment, et générez les 3 procédures de réponse aux clics sur les 3 boutons de manipulation de liste. Voici le code qu'il vous faut obtenir :
procedure TfmPrinc.btEmpileClick(Sender: TObject);
var
S: String;
begin
if InputQuery('Empilement d''une chaîne', 'Saisissez une chaîne à empiler', S) then
begin
Pile := PLEmpiler(Pile, S);
MajInterface;
end;
end;
procedure TfmPrinc.btDepileClick(Sender: TObject);
begin
Pile := PLDepiler(Pile);
MajInterface;
end;
procedure TfmPrinc.btVidePileClick(Sender: TObject);
begin
while not PLVide(Pile) do
Pile := PLDepiler(Pile);
MajInterface;
end;Déclarez également une variable Pile de type PPileElem à l'endroit où nous l'avions déclaré dans le premier projet. Insèrez la procédure "MajInterface" suivante (vous noterez que le bouton "Empiler" n'est plus désactivable puisque l'opération de test de pile pleine n'existe pas dans cette implémentation) :
procedure MajInterface;
var
vide: boolean;
begin
PLAffiche(Pile, fmPrinc.mePile.Lines);
vide := PLVide(Pile);
fmPrinc.btDepile.Enabled := not vide;
fmPrinc.btVidePile.Enabled := not vide;
end;Programmez l'action du bouton "Fermer" (un simple "Close;" suffit), générez les procédures de réponse aux événements OnCreate et OnDestroy de la fiche et complètez-les à l'aide du listing ci-dessous :
procedure TfmPrinc.FormCreate(Sender: TObject);
begin
Pile := PLNouvelle;
end;
procedure TfmPrinc.FormDestroy(Sender: TObject);
begin
PLDetruire(Pile);
end;
Voilà, vous avez votre nouveau projet complet. Si vous le lancez, vous constaterez
que son fonctionnement est rigoureusement identique au précédent, puisque les
changements se situent à un niveau dont l'utilisateur ignore tout. Vous voyez bien
par cet exemple qu'il est possible d'isoler une structure de données avec les
opérations la manipulant. Si pour une raison X ou Y vous deviez changer la
structure de données sous-jacente, les opérations de manipulation devront être
réécrites, mais si vous avez bien fait votre travail, comme nous l'avous fait
ci-dessus, le code utilisant ces opérations changera de façon anecdotique (la
majorité des changements ont consister à renommer les appels de procédures et à ne
plus faire appel à PTPleine, que l'on aurait d'ailleurs tout aussi bien pû
implémenter par une fonction qui renverrait toujours un booléen faux).
Nous nous sommes limités ici à manipuler des piles de chaînes. Mais rien ne nous
interdit de manipuler des structures plus complexes, telles des enregistrements ou
même des pointeurs. Il faudra bien faire attention à ne pas confondre dans ce
dernier cas les pointeurs servant à structurer la pile et ceux pointant vers les
éléments "stockés" dans la pile. Je donnerais un exemple de ce genre de chose dans
le paragraphe consacré aux Listes.
XV-C. Files▲
XV-C-1. Présentation et définition▲
Le deuxième type de données que nous allons étudier ici est la File. Si vous connaissez ce mot, c'est qu'il est utilisé par exemple dans l'expression "File d'attente". Une file d'attente fonctionne sur le principe suivant (s'il n'y a pas de gens de mauvaise fois dans cette file) : le premier arrivé est le premier servi, puis vient le deuxième, jusqu'au dernier. Lorsqu'une personne arrive, elle se met à la queue de la file et attend son tour (sauf si elle est pressée ou impolie, mais aucune donnée informatique bien élevée ne vous fera ce coup-là). Le type File général fonctionne sur le même principe : on commencer par créer une file vide, puis on "enfile" des éléments, lorsqu'on défile un élément, c'est toujours le plus anciennement enfilé qui est retiré de la file. Enfin, comme pour tout type abstrait, on détruit la file lorsqu'on en a plus besoin. Les opérations permises sur un type File sont :
- Création d'une nouvelle file vide
paramètres : (aucun)
résultat : file vide - Enfilement d'un élément (ajout)
paramètres : une file et un élément du type stocké dans la file
paramètres : une file et un élément du type stocké dans la file
résultat : une file contenant l'élément si la file n'était pas pleine - Défilement d'un élément (retrait)
paramètres : une file
résultat : une file dont la tête a été supprimée si la file n'était pas vide - Tête (accès à l'élément de tête)
paramètres : une file
résultat : un élément du type stocké dans la file, si elle n'est pas vide - Test de file vide qui indiquera si la file est vide ou non
paramètres : une file
résultat : un booléen (vrai si la file est vide) - Test de file pleine, qui indiquera si la capacité de la file est atteinte et qu'aucun nouvel élément ne peut être ajouté (cette opération n'est pas toujours définie, selon les implémentations).
paramètres : une file
résultat : un booléen (vrai si la file est pleine)
Il existe diverses manières d'implémenter un type file. Par exemple, il est possible d'utiliser un tableau conjugué avec deux indices de tête et de queue. Vous pourrez essayer de réaliser cela par vous-même car je n'en parlerai pas ici. Sachez seulement qu'une telle implémentation exige une case "neutre" dans le tableau. Contactez-moi si vous voulez plus de détails. Un moyen qui reste dans la lignée de ce que nous venons de faire avec les piles est une implémentation utilisant une liste chaînée.
XV-C-2. Implémentation d'une file par une liste chaînée▲
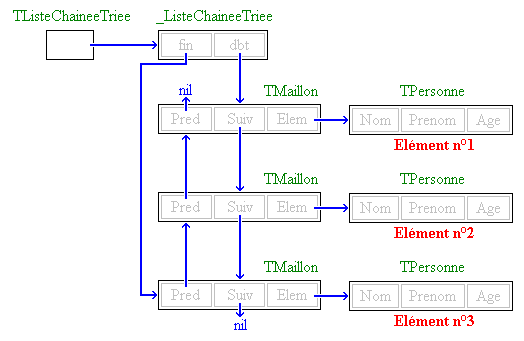
Une file peut être représentée par une liste à simple chaînage : Chaque élément
est alors un "maillon" de cette chaîne", comme pour les piles, sauf que les
opérations de manipulation seront différentes. On doit décider dés le début si
le premier élément de la liste chaînée sera la tête ou la queue de la liste.
Les deux choix sont possibles et l'un comme l'autre défavorisent une ou
plusieurs opérations : si on choisit que le premier élément désigne la tête,
c'est l' "enfilement" qui est défavorisé car il faudra "parcourir" la chaîne
(comme dans la procédure "PLAfficher" décrite plus haut) pour atteindre le
dernier élément (la queue de file). Si on choisit le contraire, ce sont les
opérations "Défiler" et "Sommet" qui sont défavorisées, pour la même raison. De
tels inconvénients pourraient être évités en utilisant un double chaînage, mais
cela consomme plus de mémoire et entraîne des complications inutiles... Nous
allons donc choisir ici la première solution, à savoir que le premier élément
sera la tête.
Nous allons écrire les types, fonctions et procédures nécessaires à la manipulation
d'une file d'attente. Voici les déclarations de types nécesaires. Il ne devrait y
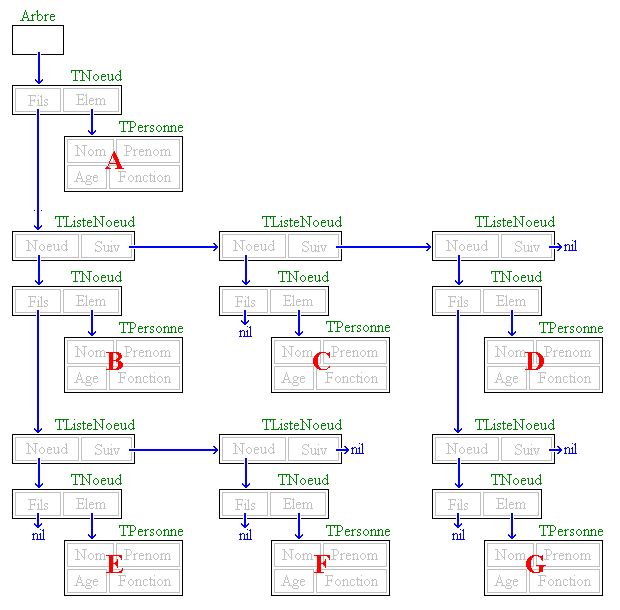
avoir aucune surprise :
type
TPersonne = record
Nom: string;
Prenom: string;
end;
PFileElem = ^TFileElem;
TFileElem = record
Elem: TPersonne;
Suiv: PFileElem;
end;On définit d'abord un type TPersonne très standard, puis un type pointeur PFileElem vers un élément de type TFileElem. TFileElem est ensuite déclaré comme étant un enregistrement, donc un "maillon" de la liste chaînée, pouvant contenir les infos d'une personne et un pointeur vers l'élément suivant de la chaîne. Comme pour une pile, une file sera représentée à l' « extérieur » par un pointeur de type PFileElem. La file vide sera représentée par un pointeur égal à nil. On introduira des éléments dans la file comme pour une pile. la tête s'obtiendra comme s'obtenait le sommet de pile. Par contre, le défilement nécessitera un parcours de la file et quelques petits tests. Voici deux fonctions très simples : FLNouvelle (création d'une file vide) et FLVide (test de file vide). Vous noterez qu'on ne peut pas utiliser l'identificateur "File" puisqu'il désigne un type fichier.
function FLNouvelle: PFileElem;
begin
result := nil;
end;
function FLVide(F: PFileElem): Boolean;
begin
result := F = nil;
end;Rien de très compliqué dans ce qui précède. Venons-en à l'enfilement d'un élément, qui est probablement la fonction la plus délicate à programmer. Le principe est de créer un nouvel élément et de l'accrocher en fin de liste chaînée. Le principe est d'utiliser une boucle while qui parcours la liste. Attention cependant, comme il nous faut pouvoir raccrocher le nouvel élément créé à la fin de la liste, il nous faut le champ "Suiv" du dernier élément. La boucle while parcours donc la liste élément par élément jusqu'à ce que le "successeur" de l'élément soit nil. Ce dernier maillon obtenu, il est ensuite facile d'y accrocher le nouveau maillon. Cette boucle while pose un problème si la liste est vide, car alors aucun champ "Suiv" n'est disponible. Dans ce cas, on effectue un traitement spécifique en retournant l'élément nouvellement créé qui devient notre file à un élément.
function FLEnfiler(F: PFileElem; Nom, Prenom: string): PFileElem;
var
f_par,
temp: PFileElem;
begin
new(temp);
temp^.Elem.Nom := Nom;
temp^.Elem.Prenom := Prenom;
// attention, fixer Suiv à nil sinon impossible de
// détecter la fin de file la prochaine fois !
temp^.Suiv := nil;
if F = nil then
result := temp
else
begin
// initialisation du parcours
f_par := F;
// parcours
while f_par^.Suiv <> nil do
// passage au maillon suivant
f_par := f_par^.Suiv;
// accrochage de temp en fin de liste.
f_par^.Suiv := temp;
result := F;
end;
end;La première partie de la fonction crée et initialise le nouveau "maillon". La seconde a pour but d'accrocher ce maillon. Deux cas se présentent : soit la file est vide (F = nil) et dans ce cas le nouvel élément créé est retourné. Sinon, après avoir initialisé un pointeur f_par, on parcours les éléments un à un jusqu'à ce que le champ "Suiv" de f_par^ soit nil, ce qui signifie alors que f_par est un pointeur vers le dernier élément. Le nouveau maillon créé précédemment est alors "accroché". Passons à l'opération de défilement :
function FLDefiler(F: PFileElem): PFileElem;
begin
if F <> nil then
begin
result := F^.Suiv;
Dispose(F);
end
else
result := F;
end;Ici, c'est un peu plus simple : si la file est vide, rien n'est fait : la file est retournée vide. Sinon, le premier élément est supprimé (la tête de file). Pour cela, le champ Suiv de F^ est affecté à Result, puis l'appel à Dispose permet de libèrer la mémoire associée à l'élément pointé par F. Le résultat est donc une file privée de son ancienne "tête". Venons-en à la fonction d'accès au sommet.
function FLSommet(F: PFileElem): TPersonne;
begin
if F <> nil then
result := F^.Elem;
end;Cette fois, aucun résultat n'est renvoyé lorsque la file est vide, ce qui donnera des résultats imprévisibles : au programmeur utilisant la fonction de faire le test avant. Sinon, on retourne directement un élément de type TPersonne, car il est impossible de retourner plusieurs résultats. Retourner un type enregistrement n'est pas très élégant (dans d'autres languages, c'est tout bonnement impossible), mais c'est aussi ce qu'il y a de plus simple. Venons-en à la procédure de suppression d'une file. C'est une procédure très standard de suppression de tous les éléments d'une liste simplement chaînée. Je n'ai pas, comme pour les piles, délégué les détails à l'opération de retrait d'un élément. Voici ce que cela donne :
procedure FLDetruire(F: PFileElem);
var
temp, sauv: PFileElem;
begin
temp := F;
while temp <> nil do
begin
sauv := temp^.Suiv;
dispose(temp);
temp := sauv;
end;
end;
le principe est d'initialiser un pointeur temporaire au pointeur de départ, et de
le faire "avancer" dans la liste chaînée en détruisant les éléments parcourus. Pour
cela, on est obligé de sauvegarder le champ "Suiv" à chaque fois car le fait de
libèrer la mémoire associée au pointeur le rend innaccessible au moment où on en a
besoin.
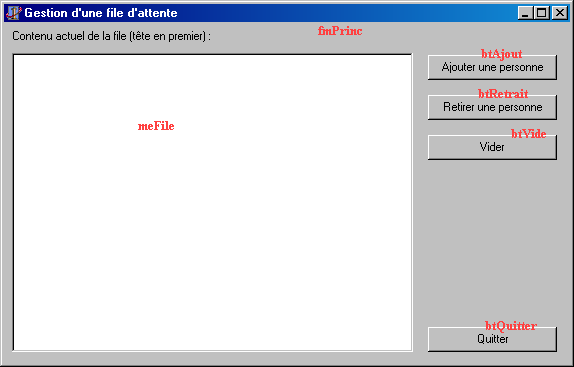
Nous allons maintenant réaliser une petite application à but purement didactique
(son intérêt, comme les deux précédentes, étant assez limité...). Créez un nouveau
projet, et ajoutez une fiche. Utilisez les captures d'écran ci-dessous pour
dessiner votre interface :
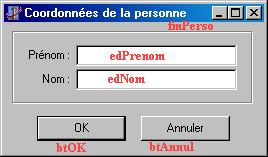
Ajoutez maintenant une unité où vous rentrerez manuellement les
types/fonctions/procédures décrites plus haut, ou alors téléchargez l'unité toute
faite ici : files_prt.pas,
ou bien encore téléchargez le projet complet : files.zip.
N'oubliez pas de rajouter l'unité de la fiche de saisie des coordonnées et celle
contenant l'implémentation du TAD File dans la clause uses de l'unité principale.
Générez la procédure associée à l'événement OnShow de la fiche de saisie des
coordonnées. Complètez le code avec ce qui suit :
procedure TfmPerso.FormShow(Sender: TObject);
begin
edNom.Text := '';
edPrenom.Text := '';
ActiveControl := edNom;
end;Ceci a pour effet de vider les zones d'édition et d'activer la zone d'édition du nom lorsque la fiche est affichée. Il nous faut maintenant initialiser et détruire la file d'attente aux bons moments. Les événements OnCreate et OnDestroy de la fiche principale sont des endroits idéaux pour cela. Générez donc les procédures associées à ces deux événements et saisissez le code source ci-dessous :
procedure TfmPrinc.FormCreate(Sender: TObject);
begin
F := FLNouvelle;
end;
procedure TfmPrinc.FormDestroy(Sender: TObject);
begin
FLDetruire(F);
end;Afin de voir l'état de la file, nous devrons régulièrement afficher son contenu dans le Mémo prévu à cet effet. Nous aurons également besoin de faire certaines mises à jour de l'interface en fonction des actions effectuées par l'utilisateur. Le plus simple pour une si petite application est une procédure "MajInterface" qui se chargera des mises à jour. Cette procédure sera appelée chaque fois que nécessaire et réalisera entre autre l'affichage de la file et l'activation de certains boutons.
procedure MajInterface;
var
vide: boolean;
begin
FLAffiche(F, fmPrinc.meFile.Lines);
vide := FLVide(F);
fmPrinc.btRetrait.Enabled := not vide;
fmPrinc.btVide.Enabled := not vide;
end;Dans la procédure ci-dessous, pour que l'affichage puisse se faire dans le mémo, on doit transmettre sa propriété "Lines" qui est bien de type "TStrings". Pour accèder à cette propriété, il nous faut bien la « qualifier » avec "fmPrinc.meFile" car la procédure est indépendante de la fiche et il faut donc commencer par accèder à celle-ci puis au mémo et enfin à la propriété "Lines". Le reste ne présente aucune difficulté. Nous pouvons maintenant nous occuper des opérations effectuées par chacun des trois boutons (je vous laisse programmer l'action du bouton "Quitter" vous-même). Le premier bouton permet de saisir une nouvelle personne et de l'insèrer dans la file d'attente. Pour saisir les coordonnées de la personne, nous aurions pû utiliser deux "InputQuery", mais cela manquerait quelque peu de convivialité. C'est pour cette raison que nous avons créé une fiche annexe servant de fenêtre de saisie. Cette fiche sera appelée par sa méthode "ShowModal" (c.f. chapitre 10 pour plus de détails) ; il faut donc fixer les propriétés "ModalResult" des deux boutons "Ok" et "Annuler" de cette fiche aux valeurs respectives de "mrOk" et "mrCancel". Une petite précaution réalisée ci-dessus nous permet de vider automatiquement les zones de saisie et de réactiver la zone de saisie de nom (car sinon ce serait le bouton cliqué lors de la dernière utilisation qui serait activé) à chaque nouvelle utilisation de cette fiche.
procedure TfmPrinc.btAjoutClick(Sender: TObject);
begin
// si l'utiliasteur a cliqué sur OK dans la fenêtre de saisie
if fmPerso.ShowModal = mrOK then
begin
// Enfilement d'un nouvel élément
F := FLEnfiler(F, fmPerso.edNom.Text, fmPerso.edPrenom.Text);
// Mise à jour de l'interface pour reflèter ce changement
MajInterface;
end;
end;
On commencer par afficher la fiche de saisie. Comme on doit tester le résultat de
l'appel à "ShowModal", on met cet appel dans un bloc if qui compare la valeur de
retour à "mrOK". Si c'est la valeur de retour, l'utilitaire a confirmé les
coordonnées et l'ajout dans la file peut être fait. Pour cela, on utilise la
fonction "FLEnfiler" et on transmet la file et les champs "Text" des composants
"edNom" et "edPrenom" de la fiche de saisie "fmPerso". Le résultat est réaffecté à
F. Enfin, l'interface est mise à jour, ce qui permet d'afficher le nouveau contenu
de la file. Vous verrez que le nouvel élément s'ajoute à la suite des autres
contrairement au cas d'une pile où il s'affichait avant tous les autres.
Le bouton "Retirer une personne" permet de défiler un élément. Ce bouton n'est
activé que lorsque la file n'est pas vide. En fait, ce n'est pas tout à fait le
cas, car lors du lancement de l'application, ce bouton est activé alors qu'il ne
devrait pas l'être. Changez cet état de fait en fixant les propriétés "Enabled" des
boutons "btRetrait" et "btVide" en "false". Les instructions éxécutées par un clic
sur ce bouton sont assez simples.
procedure TfmPrinc.btRetraitClick(Sender: TObject);
begin
F := FLDefiler(F);
MajInterface;
end;La première instruction défile (l'élément de tête). La seconde met l'interface à jour. Venons-en enfin à l'action du bouton "Vider" :
procedure TfmPrinc.btVideClick(Sender: TObject);
begin
while not FLVide(F) do
F := FLDefiler(F);
MajInterface;
end;Le code ci-dessus vide la file dans le sens où il défile élément par élément tant que la file est non vide. L'interface est ensuite mise à jour. Si vous avez suivi toutes les explications ci-dessus, vous êtes maintenant en possession d'un projet en état de fonctionner. Lancez-le, ajoutez des personnes, retirez-en, en notant la différence par rapport aux piles. Si vous n'avez pas réussi une ou plusieurs des étapes ci-dessus, vous pouvez télécharger le code source complet du projet ici : files.zip. Nous allons maintenant passer aux listes.
XV-D. Listes▲
XV-D-1. Présentation et définition▲
La notion de liste d'éléments est une notion très naturelle dans le sens où nous
manipulons des listes assez régulièrement, ne serait-ce que lorsque nous faisons
notre liste de courses (liste d'articles) ou lorsque nous consultons un extrait
de compte (liste d'opérations bancaires). Ces listes famillières cachent
cependant plusieurs concepts : comment sont-elles construites, leur
applique-t-on un tri ? Quel ordre dans ce cas ? Pour un extrait de compte, c'est
simplement un ordre chronologique, dans de nombreux cas ce sera un tri numérique
(à partir de nombres), alphabétique (à partir de lettres) ou plus souvent
alphanumérique (lettres et chiffres). Les listes étant souvent plus
intéressantes lorsqu'elles sont triées, ce paragraphe présente un TAD Liste
trié. Il est assez simple de réaliser un type non trié en éliminant tout ce qui
se rapporte au tri dans ce qui suit. Nous allons faire un détour préliminaire
par les notions de tri dont la difficulté est souvent sous-estimée avant de nous
attaquer à deux manières d'implémenter les listes triées.
Au niveau abstrait, une liste est une collection d'objets de même nature dans
lequel il peut y avoir des redondances. Si on veut éviter ce cas, on peut
directement l'interdire ou l'autoriser au moment de la programmation. On peut aussi
dans ce dernier cas créer une liste dite d' «, occurrences » qui contiendra en plus
de l'élément son nombre d'occurrences (au lieu d'ajouter deux fois "toto", on
ajoutera "toto" une fois avec une valeur 2 (dite de comptage) associée). Une liste
peut être triée ou non. Il existe des nuances, comme les listes non triées sur
lesquelles on peut opèrer un tri spécifique au moment voulu : La classe TList
fournie par Delphi permet de gèrer ce genre de liste. Nous parlerons ici d'abord
des listes triées directement lors de l'insertion des éléments, ce qui impose un
ordre de tri fixé, puis nous modifierons l'une de nos implémentations pour
permettre différents types de tris sur les éléments. Contrairement aux piles et aux
files dans lesquelles l'emplacement d'insertion et de retrait des éléments
est fixée, la position d'insertion dépend exclusivement de l'ordre de tri
pour les listes triées, et la position de retrait est imposée par l'élément qu'on
souhaite supprimer (élément qu'on devra explicitement indiquer). La suppression ne
devra pas non plus interfèrer sur le tri.
Au niveau de l'implémentation des listes, il existe plusieurs possibilités parmi
lesquelles :
- les tableaux
- les listes à simple chaînage
- les listes à double chaînage
Bien que la première soit la plus simple, nous avons déjà vu son principal
inconvénient et son principal avantage : respectivement une taille fixe en
contrepartie d'une plus grande facilité d'implémentation. La deuxième
possibilité utilise une liste à simple chaînage, ce qui peut se révèler plus
intéressant mais un peu lourd ; de plus, vous venez de voir deux
implémentations utilisant le chaînage simple et il est temps de passer à
l'étape suivante : la liste à double, qui est la solution idéale pour les
listes triées Ces listes sont plus pratique à utiliser mais moins évidentes à
faire fonctionner. Nous utiliserons la première et la troisième possibilité
essentiellement pour éviter de tomber dans la répétition. Après une
présentation théorique, la suite du cours sera divisée en quatre : la première
partie (§ 4.2) aborde des notions sur les tris. La deuxième (§ 4.3) présente
une implémentation d'une liste "triée à l'insertion" par un tableau. La
troisième (§ 4.4) présente une implémentation par une liste
doublement chaînée. Enfin, une quatrième section (§ 4.5) viendra améliorer la
précédente implémentation (§ 4.4) en supprimant le tri à l'insertion des éléments et
en permettant d'effectuer un tri arbitraire sur les éléments).
Un peu de théorie maintenant. Lorsqu'on souhaite utiliser une liste, il faudra
commencer par l'initialiser. Ensuite, un certain nombre d'autres opérations
classiques seront possibles, parmi lesquelles l'ajout, la suppression (en
spécifiant l'élément), l'obtention d'un élément par son numéro et le nombre
d'éléments. Toutes ces opérations maitiendront un ordre décidé à l'avance pour les
éléments. Ceci impose évidemment qu'un ordre soit choisi dans l'ensemble des
éléments. Pour ceux qui n'ont pas fait une licence de mathématiques, cela signifie
simplement qu'en présence de deux éléments, on devra pouvoir dire lequel doit être
classé avant l'autre. La dernière opération réalisée sur une liste devra être sa
suppression. Une opération de test de présence d'un élément dans une liste sera
également nécessaire. Dans la pratique, ce modèle théorique pourra être adapté aux
nécessités du moment en permettant par exemple la suppression d'un élément en
donnant son numéroau lieu de l'élément lui-même, ce qui est souvent beaucoup plus simple.
Voici les opérations possibles sur un TAD Liste triée :
- Création d'une nouvelle liste vide
paramètres : (aucun)
résultat : liste vide - Destruction d'une liste
paramètres : une liste
résultat : (aucun) - Ajout d'un élément
paramètres : une liste, un élément du type stocké dans la liste
résultat : une liste contenant l'élément : cette opération classe l'élément à sa place parmi les autres. - Suppression d'un élément
paramètres : une liste, un élément du type stocké dans la liste
résultat : une liste où l'élément transmis a été supprimé
(Note : on se permettra souvent, dans la pratique de remplacer l'élément par son numéro) - Nombre d'éléments
paramètres : une liste
résultat : un entier indiquant le nombre d'éléments dans la liste - Accès à un élément
paramètres : une liste, un entier
résultat : sous réserve de validité de l'entier, l'élément dont le numéro est transmis
Comme d'habitude, nous ajouterons une procédure permettant d'afficher le contenu de la liste dans un mémo. Nous conviendrons que les listes que nous allons manipuler tolèrent les répétitions et que les éléments sont numérotés à partir de 0 (lorsqu'on aura n éléments, ils seront accessibles par les indices 0 à n-1).
XV-D-2. Notions de tri▲
Si vous êtes débutant en programmation (j'espère que vous l'êtes maintenant un peu
moins grâce à moi ;-), vous vous demandez sûrement pourquoi je consacre un
paragraphe aux tris. En effet, nous avons tous une notion assez intuitive du tri
que l'ordinateur ne connait absolument pas. Prenons par exemple la liste suivante :
1276, 3236, 2867, 13731, 138, 72, 4934. Je vous faciliterai la vie, certainement,
en vous la présentant comme ceci :
1276
3236
2867
13731
138
72
4934
Mais l'ordinateur, lui, ne fera pas cette petite présentation pour y voir plus
clair. Si je vous demande maintenant de classer cette liste dans l'ordre
décroissant, vous allez procèder à votre manière (pensez que d'autres pourraient
procèder autrement) et me répondre après rèflexion :
13731
4934
3236
2867
1276
138
72
Arrêtons nous un instant sur la méthode que vous venez d'employer : avez-vous
raisonné de tête ou sur papier ? avec le bloc-notes de Windows peut-être ?
L'ordinateur, lui, n'a aucune idée de ce que tout cela représente. Avez-vous
été contrarié que je demande l'ordre décroissant et non l'ordre croissant ?
Même pas un tout petit peu ? L'ordinateur, lui, ne se contrariera pas. Vous
avez probablement cherché d'abord le plus grand élément (vous savez reconnaître
le "plus grand" élément parce que je vous ai dit que l'ordre était
décroissant). Pour obtenir ce plus grand élément, vous avez très probablement
triché : vous avez en une vision d'ensemble des valeurs, comportement que j'ai
d'ailleurs encouragé en vous présentant les valeurs d'une manière propice.
L'ordinateur, lui, n'a pas de vision d'ensemble des données. Mais examinons
plus avant votre raisonnement : vous avez vu un premier élément, vu qu'un autre
était plus grand (vous avez donc "comparé" les deux valeurs, ce qui n'est pas
forcément évident pour un ordinateur), et donc abandonné le premier au bénéfice
du second, et répété ceci jusqu'à avoir parcouru la liste entière : c'est la
seule et unique méthode, même si on pourrait lui trouver des variantes.
Une fois cette valeur trouvée, qu'en avez-vous fait ? Si vous êtiez sur papier,
vous avez probablement recopié la valeur puis barré dans la liste. Ce faisant, vous
avez entièrement reconstruit la liste : pensez à l'occupation mémoire de votre
feuille de papier : si vous n'avez pas optimisé, vous avez maintenant une liste
entièrement barrée (qui prend de la place, donc de la mémoire), et une liste toute
neuve, qui prend autant de place que son homologue déchue. N'aurait-il pas été plus
intelligent de localiser le premier élément (le "plus grand"), puis de le permuter
avec le premier de la liste pour le mettre à sa place définitive, et de continuer
avec le reste de la liste ? Si vous avez travaillé avec le bloc-notes de Windows,
vous avez probablement appliqué une troisième méthode : après avoir localisé le
"plus grand" élément, vous avez "coupé" la ligne, puis l'avez "collée" en tête,
décalant ainsi les autres éléments.
Si je vous fait ce petit discours qui ressemble davantage à de l'analyse de
comportement qu'à de l'informatique, c'est pour vous montrer combien l'ordinateur
et vous êtes inégaux devant les tris de données. Et encore, je ne vous ai pas parlé
de voitures à trier par ordre de préférence... Comprenez bien que si pour vous le
tri de données est affaire d'intelligence/d'organisation, et de temps si la liste
est longue, il en est de même pour l'ordinateur, à ceci près que lui se contente
d'exécuter des programmes alors que vous avez un cerveau. Le principal problème,
lorsqu'on s'attaque aux tris informatisés, c'est leur vitesse. Lorsque vous êtes
sous Microsoft Excel, tolèreriez-vous qu'un tri sur 10000 lignes prenne 2 heures ?
Bien sûr que non. Or, si nous faisions l'expérience de traduire en language
informatique ce que vous venez de faire avec la petite liste de valeurs, on serait
très probablement assez proches de cet ordre de grandeur (ce serait long !).
Pour accélérer les choses, informaticiens et mathématiciens ont travaillé
d'arrache-pied et mis au point des techniques, aussi appelées algorithmes par les
afficionados. Ces algorithmes permettent en théorie de diminuer le temps nécessaire
aux tris (quoique dans certaines situations très particulières, certains
algorithmes "pètent les plombs" et font perdre du temps !). Parmi les méthodes qui
existent, j'ai choisi d'en présenter 4 : le tri par Sélection, le tri à Bulles
("BubbleSort"), le tri Rapide ("QuickSort") et le tri Shell ("ShellSort"). Ces
quatres méthodes sont envisageables pour des listes peu volumineures, mais seules
les deux dernières (la première est enviseagable mais à éviter) sont à prescrire
pour les listes volumineuses. Les deux dernières méthodes utilisent des algorithmes
assez complexes et je n'entrerai donc pas dans les détails, histoire de ne pas vous
noyez dans des détails techniques. A la place, j'expliquerai l'idée générale de la
méthode.
Toutes ces méthodes permettent de séparer la partie "intelligence" (l'algorithme,
exprimé sous formes d'instructions Pascal), des traitements mécaniques. Ces
derniers sont réduits au nombre de deux : la comparaison de deux éléments, et la
permutation de deux éléments. En séparant ainsi l'"intelligence" de la partie
"mécanique", on se complique certes un peu la vie, mais on se donne la possibilité
d'utiliser la partie "intelligence" avec divers types de données, uniquement
identifiés au niveau "mécanique". Pour vous faire comprendre ceci, pensez aux
impôts sur le revenu : l'état les collecte, et délègue les détails de la collecte :
l'état est dans notre exemple la partie "intelligence". Pour chacun d'entre nous,
payer les impôts sur le revenu passe par une déclaration au format papier : c'est
la partie "mécanique" de l'exemple. Imaginez demain que nous faisions tous cette
déclaration sur Internet, il n'y aurait plus de papier, et donc la partie
"mécanique" changerait, mais la partie "intelligence" resterait inchangée :
l'impôt sera toujours collecté.
Pour en revenir à l'informatique, le tri par Sélection est celui qui se rapproche
le plus de ce que nous faisons habituellement. Le principe est à chaque étape
d'identifier l'élément à placer en tête de liste, et de permuter le premier élément
de la liste avec cet élément. On poursuit le tri en triant uniquement le reste de
la liste de la même manière (si la liste contenait n éléments, on trie les n-1
derniers éléments). Voici un tableau montrant les diverses étapes de ce genre de
tri sur notre petite liste d'éléments, avec à chaque fois mentionné le nombre de
comparaisons nécessaires :
| 1276 | 72 | 72 | 72 | 72 | 72 | 72 |
| 3236 | 3236 | 138 | 138 | 138 | 138 | 138 |
| 2867 | 2867 | 2867 | 1276 | 1276 | 1276 | 1276 |
| 13731 | 13731 | 13731 | 13731 | 2867 | 2867 | 2867 |
| 138 | 138 | 3236 | 3236 | 3236 | 3236 | 3236 |
| 72 | 1276 | 1276 | 2867 | 13731 | 13731 | 4934 |
| 4934 | 4934 | 4934 | 4934 | 4934 | 4934 | 13731 |
| comparaisons | 6 | 5 | 4 | 3 | 2 | 1 |
On arrive à la liste triée avec 6 permutations et 21 comparaisons, ce qui peut
paraître bien, mais qui aura tendance à grimper de manière dramatique : avec 10000
éléments, il faudrait 9999 permutations et 49985001 comparaisons.
Le tri à Bulles fonctionne sur un principe différent et son algorithme est des plus
faciles à comprendre : la liste est considèrée comme des éléments placés de haut
(tête de liste) en bas (queue de liste), un peu comme sur du papier ou un écran
d'ordinateur. On parcours la liste du "bas" vers le "haut" (le "haut" s'abaissera
d'un élément à chaque fois puisqu'à chaque itération, l'élément arrivant en
première position est trié) et à chaque étape, un élément, considéré comme une
"bulle", est remonté en début de liste : comme une bulle qui remonterait à la
surface de l'eau, on remonte progressivement dans la liste et dés que deux éléments
consécutifs sont dans le désordre, on les permute (sinon on ne fait rien et on
continue à remonter). En fait, à chaque parcours, plusieurs éléments mal triés sont
progressivement remontés à une place temporaire puis définitive au fil des
itérations. Voici ce que cela donne avec notre petite liste, mais uniquement pour
la première itération :
Etape 1 : remontée de la bulle n°1 : on regarde 4934 (élément n°7) 4934 et 72 sont
mal triés, on les permute. On regarde l'élément n°6 : 4934 et 138 sont mal triés,
on les permute. On regarde l'élément n°5 : 4934 et 13731 sont bien triés. On
regarde l'élément n°4 : 13731 et 2867 sont mal triés, on les permute. On regarde
l'élément n°3 : 3236 et 13731 sont mal triés, on les permute. On regarde l'élément
n°2 : 1276 et 13731 sont mal triés, on les permute.
| 1276 | 1276 | 1276 | 1276 | 1276 | 13731 |
| 3236 | 3236 | 3236 | 3236 | 13731 | 1276 |
| 2867 | 2867 | 2867 | 13731 | 3236 | 3236 |
| 13731 | 13731 | 13731 | 2867 | 2867 | 2867 |
| 138 | 138 | 4934 | 4934 | 4934 | 4934 |
| 72 | 4934 | 138 | 138 | 138 | 138 |
| 4934 | 72 | 72 | 72 | 72 | 72 |
Comme vous le voyez, le premier élément, 13731, est bien trié (il est à sa place
définitive). A l'étape suivante, on appliquera la méthode aux six derniers éléments
et ainsi de suite jusqu'à avoir trié toute la liste. Comme vous vous en rendez
probablement compte, les performances de cet algorithme ne sont vraiment pas
excellentes et il ne vaut mieux pas dépasser quelques centaines d'éléments sous
peine de mourrir d'ennui devant son ordinateur.
L'algorithme du Tri Shell, généralement plus rapide que le tri par sélection,
compare d'abord des éléments éloignés de la listr à trier, puis réduit l'écart
entre les éléments à trier, ce qui diminue très rapidement le nombre de
comparaisons et de permutations à effectuer. L'application en téléchargement
ci-dessous implémente un tri shell sur un tableau d'entiers. Je parle de cette
application un peu plus bas. Le tri Rapide, enfin, utilise une technique de
"partition" de la liste à trier : un élément "pivot" est choisi dans la liste et
les éléments se retrouvant du mauvais coté de ce pivot sont permutés, puis chaque
moitié est triée à son tour. Cet algorithme est un des plus rapides, mais il arrive
qu'il "dégénère", c'est-à-dire qu'il mette un temps incroyablement long à trier peu
d'éléments.
Pour que vous puissiez observer et juger par vous-même les différentes méthodes de
tri abordées ici, je vous ai concocté une petite application. Téléchargez le code
source du projet, examinez-le un peu, et essayez les divers tris (un petit
conseil : évitez plus de 300 valeurs pour le BubbleSort et 3000 pour le tri par
Sélection). N'hésitez pas à modifier le code source à votre guise ou à réutiliser
des morceaux de code dans vos applications.
Le but de ce paragraphe étant avant tout de vous initier à la dure réalité des tris
de données, je n'entre pas dans trop de détails techniques pas plus que je ne donne
les algorithmes des méthodes évoquées. Internet regorge d'exemples et
d'implémentations de chacun de ces tris. Sachez enfin que la méthode Sort de la
classe TList utilise la méthode QuickSort pour trier les données. Pour fonctionner,
cette méthode a besoin que vous lui donniez le nom d'une fonction de comparaison.
Ce genre de pratique étant encore un peu délicate à comprendre, je la réserve pour
plus tard (§ 4.5).
XV-D-3. Implémentation par un tableau▲
Nous allons réaliser une première implémentation d'une liste triée. Le type de tri sera figé et donc effectué lors de l'iinsertion des éléments. Nous allons ici utiliser un tableau pour stocker les éléments de la liste, tout en essayant d'adopter une structure de données plus élaborée que celles utilisées pour les piles et les files. Voici les types utilisés :
const
MAX_ELEM_LISTE_TRIEE = 200;
type
// un type destiné à être stocké dans la liste
TPersonne = record
Nom, Prenom: string;
Age: integer;
end;
// ElemListe pourraît être changé sans trop de difficultés
PPersonne = ^TPersonne;
// enreg. contenant une liste triée
_ListeTabTriee = record
// nombre d'éléments
NbElem: integer;
// éléments (pointeurs)
Elem: array[1..MAX_ELEM_LISTE_TRIEE] of PPersonne;
end;
{ le vrai type : c'est un pointeur, beaucoup plus indiqué
qu'un simple enregistrement ou un tableau. }
TListeTabTriee = ^_ListeTabTriee;
Le premier type ci-dessus (TPersonne), est choisi arbitrairement pour cet
exemple. Nous utilisons un type intermédiaire nommé PPersonne qui est un
pointeur vers un élément de type TPersonne. Les éléments stockés seront donc
non pas réellement les éléments de type TPersonne mais des pointeurs vers ces
éléments. Le type utilisé pour implémenter la liste est un enregistrement. Le
champ NbElem nous permettra de mémoriser le nombre d'éléments présents dans la
liste. Le tableau Elem stockera les pointeurs de type PPersonne vers les
éléments de type TPersonne. Il faut savoir que le choix effectué pour les piles
et les files d'utiliser un type enregistrement seul n'est en fait pas une très
bonne idée. Il est préférable d'utiliser un pointeur vers un tel élément. Le
type utilisé sera alors TListeTabTriee qui est un pointeur vers un
enregistrement stockant une liste triée.
Nous allons maintenant implémenter les diverses opérations de manipulation d'un tel
type de donnée. En tout premier, les deux opérations de création et de destruction
d'une liste :
function LTTNouvelle: TListeTabTriee;
begin
new(result);
result^.NbElem := 0;
end;
procedure LTTDetruire(Liste: TListeTabTriee);
var
i: integer;
begin
if Liste <> nil then
begin
for i := 1 to Liste^.NbElem do
Dispose(Liste^.Elem[i]);
Dispose(Liste);
end;
end;
Dans le code ci-dessus, un élément de type _ListeTabTriee est créé par New, puis le
nombre d'éléments est initialisé à 0. Du fait de l'utilisation de pointeurs, aucune
autre action initiale comme une allocation de mémoire n'est nécessaire. La
suppression commence par vérifier que la liste transmise n'est pas le pointeur
nil (c'est la seule chose qu'on peut tester facilement quant à la validité
de la liste) puis, dans ce cas, commence par libèrer toute la mémoire allouée aux
éléments de type TPersonne (nous choisissons de gèrer la mémoire associée aux
éléments de la liste depuis les opérations de manipulation, ce qui évite, depuis
l'extérieur, des allocations mémoire fastidieuses). Enfin, la mémoire associée à
l'élément de type _ListeTabTriee est libérée à son tour (comprenez bien qu'on ne
peut pas faire cela au début, car sinon plus d'accès possible aux pointeurs vers
les éléments qu'on souhaite retirer de la mémoire).
Passons aux opérations de Compte d'élément, de test de liste vide ou pleine. Ces
opérations sont très simples :
function LTTCompte(Liste: TListeTabTriee): integer;
begin
// on prend comme convention -1 pour une liste incorrecte
if Liste = nil then
result := -1
else
result := Liste^.NbElem;
end;
function LTTVide(Liste: TListeTabTriee): boolean;
begin
result := true;
if Liste <> nil then
result := Liste^.NbElem = 0;
end;
function LTTPleine(Liste: TListeTabTriee): boolean;
begin
result := true;
if Liste <> nil then
result := Liste^.NbElem = MAX_ELEM_LISTE_TRIEE;
end;La première opération retourne -1 si le pointeur transmis est incorrect, ou renvoie la valeur du champ NbElem dans le cas contraire. La seconde renvoie vrai si la valeur NbElem est égale à 0. Enfin, la troisième renvoie vrai si NbElem vaut la valeur maximale fixée par la constante MAX_ELEM_LISTE_TRIEE. Passons tout de suite à l'insertion d'un élément. L'insertion se fait en trois étapes : un emplacement mémoire est créé pour stocker l'élément transmis. Cet élément sera référencé par un pointeur stocké dans le tableau Elem de la liste. La seconde étape consiste à déterminer la position d'insertion de l'élément dans la liste. Enfin, la troisième étape consiste en l'insertion proprement dite. Voici la procédure complète, que j'explique ci-dessous, ainsi que la fonction de comparaison de deux éléments de type TPersonne :
// fonction de comparaison de deux "personnes"
function CompPersonnes(P1, P2: PPersonne): integer;
begin
// 0 est le résultat par défaut
result := 0;
// si erreur dans les paramètres, sortie immédiate
if (P1 = nil) or (P2 = nil) then exit;
// on compare d'abord les noms
result := AnsiCompareText(P1^.Nom, P2^.Nom);
// s'ils sont égaux, on compare les prénoms
if result = 0 then
result := AnsiCompareText(P1^.Prenom, P2^.Prenom);
// s'ils sont égaux, c'est l'écart d'âge qui fixe le résultat
if result = 0 then
result := P1^.Age - P2^.Age;
end;Cette fonction retourne un résultat négatif si le nom de P1 est "inférieur" à celui de P2 au sens de la fonction "AnsiCompareText". Si vous consultez l'aide de cette fonction, vous constaterez qu'elle fait tout le travail de comparaison et sait comparer des valeurs alphanumériques. AnsiCompareText(A, B) retourne un résultat inférieur à 0 si A < B et un résultat positif sinon. Un résultat nul est obtenu en cas d'égalité. On compare d'abord les noms, puis en cas d'égalité les prénoms, et enfin les âges au moyen d'une simple soustraction (résultat encore négatif si A < B).
function LTTAjout(Liste: TListeTabTriee; Pers: TPersonne): TListeTabTriee;
var
PersAj: PPersonne;
PosInser, i: integer;
begin
result := Liste;
if Liste = nil then exit;
// liste pleine, impossible d'ajouter un élément
if Liste^.NbElem = MAX_ELEM_LISTE_TRIEE then exit;
// création de l'élément
New(PersAj);
PersAj^ := Pers;
// recherche de la position d'insertion
if Liste^.NbElem = 0 then
PosInser := 1
else
begin
PosInser := Liste^.NbElem + 1; // Inséré par défaut en fin de liste
// diminue la position jusqu'à ce qu'un élément rencontré soit inférieur strictement
while (PosInser > 1) and (CompPersonnes(PersAj, Liste^.Elem[PosInser - 1]) < 0) do
dec(PosInser);
end;
{ deux cas sont possibles :
1) l'élément est inséré en fin de liste et alors tout va bien
2) l'élément doit être inséré à la place occupée par un autre élément, il faut
donc décaler les éléments suivants pour libèrer une place }
if PosInser <= Liste^.NbElem then
// décalage des éléments
for i := Liste^.NbElem downto PosInser do
Liste^.Elem[i+1] := Liste^.Elem[i];
// insertion
Liste^.Elem[PosInser] := PersAj;
Inc(Liste^.NbElem);
end;
Les 5 premières instructions font la première étape et quelques tests d'usage,
entre autres, si la liste est pleine, l'ajout est refusé. Une zone mémoire est créé
(new) et initialisée (affectation). Le bloc if se charge de déterminer la
position d'insertion de l'élément. Si la liste est vide, la position est 1, sinon,
on part de l'hypothèse de l'insertion en fin de liste, puis on décroit cette
position jusqu'à rencontrer un élément précédent cette position et qui soit
inférieur à l'élément à insèrer. Ainsi, si la liste contenait des nombres (1, 3 et
7 par exemple) et si on désirait insèrer 2, la position d'insertion sera celle de
3.
La troisième et dernière étape effectue, sauf cas d'ajout en fin de liste, un
décalage des pointeurs pour libèrer une place à celui qui doit être inséré. Notez
l'ordre de parcours et les éléments parcourus : un parcours dans l'ordre inverse
aurait des conséquences fâcheuses (essayez sur papier, vous verrez que les éléments
sont tous supprimés avant d'être lus). Enfin, l'élément est placé dans le tableau
d'éléments. Notez que cette méthode d'ajout est optimisable car la recherche dans
une liste triée peut s'effectuer beaucoup plus rapidement que dans une liste non
triée. Ainsi, une recherche dichotomique pourrait gagner énormément de temps sur de
grosses listes, mais comme nous nous limitons à 200 éléments, ce n'est pas assez
intéressant.
Nous avons également besoin d'une fonction permettant de supprimer un élément de la
liste. Pour simplifier, puisqu'il nous serait difficile de fournir l'élément à
supprimer, on fournit plutôt son numéro. Voici la fonction qui réalise cela :
function LTTSupprIdx(Liste: TListeTabTriee; index: integer): TListeTabTriee;
var
i: integer;
begin
result := Liste;
if Liste = nil then exit;
if (index < 1) or (index > Liste^.NbElem) then exit;
Dispose(Liste^.Elem[index]);
for i := index to Liste^.NbElem - 1 do
Liste^.Elem[i] := Liste^.Elem[i+1];
Dec(Liste^.NbElem);
end;
Les premières instructions effectuent quelques vérifications. L'élément à supprimer
est ensuite libéré de la mémoire, puis les éléments suivants dans le tableau sont
décalés pour combler la place laissée vide par l'élément supprimé.
Enfin, voici les fonctions et procédures permettant l'affichage du contenu de la
liste dans une "ListBox" ou un "Memo" :
// fonction renvoyant une chaîne décrivant une personne
function AffichPers(P: PPersonne): string;
begin
if P = nil then
result := ''
else
result := P^.Nom + ' ' + P^.Prenom + ' (' + IntToStr(P^.Age) + ' ans)';
end;
procedure AfficheListe(Liste: TListeTabTriee; Sortie: TStrings);
var
i: integer;
begin
Sortie.Clear;
if Liste = nil then
Sortie.Add('(Liste incorrecte)')
else
for i := 1 to Liste^.NbElem do
Sortie.Add(AffichPers(Liste^.Elem[i]));
end;
L'affichage d'une personne est effectué via une fonction qui crée une chaîne à
partir d'une personne. Cette chaîne est ensuite générée pour chaque personne et
ajoutée comme d'habitude à la sortie de type TStrings. Venons-en maintenant au
programme de test. Pour plus de facilité, téléchargez-le
maintenant et suivez à partir du code source, car je ne vais décrire que ce
qui est essentiel à la compréhension de l'utilisation des listes.
L'interface est très conventionnelle. Notez cependant que le mémo que nous
utilisions auparavant a été remplacé par une zone de liste (ListBox) permettant
d'avoir facilement accès au numéro de ligne sélectionnée (propriété ItemIndex). Une
petite fiche de saisie des coordonnées d'une personne fait également partie de
l'interface. Une variable "Lst" de type TListeTabTriee a été déclarée dans l'unité
de la fiche principale du projet. Remarquez, si vous avez lu le chapitre concernant
les objets, qu'on aurait tout aussi bien pû faire de cette variable un champ de
l'objet fmPrinc. J'ai choisi de ne pas le faire tant que je n'aurai pas abordé les
objets de manière plus sérieuse.
Comme dans les précédents projets exemple, une procédure MajInterface a pour charge
de mettre l'interface principale à jour en réactualisant le contenu de la liste et
en dés(activant) les boutons nécessaires. La procédure associée au bouton "Ajouter"
affiche d'abord la fenêtre de saisie (l'événement OnShow de cette fiche se charge
de la réinitialiser à chaque affichage), puis récupère les valeurs saisies pour en
faire un élément de type TPersonne, transmis à l'opération d'ajout. Les procédurs
associées aux événements OnCreate et OnDestroy de la fiche principale permettent
respectivement d'initialiser et de détruire la liste Lst. Pour retirer un élément,
il faut le sélectionner et cliquer sur "Supprimer". L'action de ce bouton consiste
à tester la propriété ItemIndex de la liste (valeur -1 si aucun élément
sélectionné, numéro commencant à 0 sinon) et selon le cas supprime ou affiche un
message d'erreur. Le bouton permettant de vider la liste se contente de supprimer
les éléments en commençant par le dernier. J'ai un peu exagéré les choses pour
vous montrer ce qu'il vaut mieux éviter de faire : cette méthode de suppression
tient presque compte de la structure interne de la liste, ce qui est fort
regretable. Vous pouvez corriger cela à titre d'exercice et me contacter en cas
de problème.
Voilà pour l'implémentation sous forme de tableau. Vous avez peut-être trouvé le
rythme un peu élevé, mais il est nettement plus important de comprendre les
mécanismes de base et les notions abstraits plutôt que les détails d'une
implémentation.
XV-D-4. Implémentation par une liste chaînée▲
Nous allons reprendre la même interface de test que précédemment sans changer
beaucoup de code concernant les listes. L'unité utilisée va être réécrite
complètement en utilisant le procédé de double chaînage, histoire à la fois de vous
donner une autre implémentation d'une liste triée mais aussi de vous familiariser
avec cette notion (pas si évidente que ça) qu'est le double chaînage. La liste
"Lst" sera déclarée d'un nouveau type, les procédures et fonctions vont également
changer un tout petit peu de nom, mais il ne devrait pas y avoir grand changement.
Je vais me permettre un petit complément de cours concernant le double chaânage
pour ceux à qui cette notion est étrangère.
Le double chaînage est, dans les grandes lignes, un simple chaînage dans les deux
sens. Contrairement au simple chaînage où chaque pointeur ne pointe que sur
l'élément suivant dans la liste, avec le procédé de double chaînage, chaque élément
pointe à la fois vers un élément "précédent" et vers un élément "suivant" (les deux
exceptions sont le premier et le dernier élément. Il est possible, en « raccordant
» la fin et le début d'une liste à double chaînage, d'obtenir une liste circulaire
très pratique dans certains cas, mais c'est hors de notre propos.
Concrêtement, voici une déclaration en Pascal Objet d'un « maillon » d'une liste à
double chaînage simplifiée (les éléments stockés sont des entiers, qu'on remplacera
par la suite par des pointeurs, histoire d'attaquer un peu de vrai programmation ;-)
type
PMaillon = ^TMaillon;
TMaillon = record
Elem: integer;
Suiv: PMaillon;
Pred: PMaillon;
end;Vous voyez que l'on déclare un pointeur général, puis que l'élément pointé par le pointeur peut a son tour contenir deux pointeurs vers deux autres éléments. Ce genre de maillon, tel quel, n'est pas très utile, utilisons donc un élément de type PPersonne à la place de l'entier et déclarons un type utilisable de l'extérieur :
type
// un type destiné à être stocké dans la liste
PPersonne = ^TPersonne;
TPersonne = record
Nom, Prenom: string;
Age: integer;
end;
// Maillon d'une liste à double chaînage
PMaillon = ^TMaillon;
TMaillon = record
Elem: PPersonne;
Suiv: PMaillon;
Pred: PMaillon;
end;
// Une liste à double chaînage sera représentée par un pointeur vers le premier élement.
TListeChaineeTriee = ^_ListeChaineeTriee;
_ListeChaineeTriee = record
Dbt: PMaillon;
Fin: PMaillon;
end;Voici une représentation plus intuitive d'une liste vide sous forme de schémas. Vous pouvez voir l'élément de type TListeChaineeTriee intialisée et pointant vers un élément _ListeChaineeTriee également initialisé (champs Dbt et Fin à nil) :
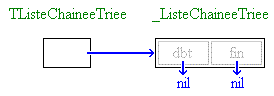
Voici maintenant le schémas d'un chaînon non initialisé : son champ Elem ne pointe sur rien et ses champs Suiv et Pred non plus :
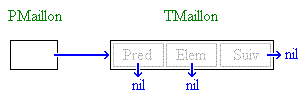
Enfin, voici le schémas d'un maillon dont le champ Elem est initialisé et pointe donc sur un élément de type TPersonne. Notez que le pointeur de type PPersonne n'est plus une variable à part mais un champ du maillon. Cependant, les champs Pred et Suiv ne sont pas encore initialisé, car ce maillon n'est pas encore intégré à une liste.
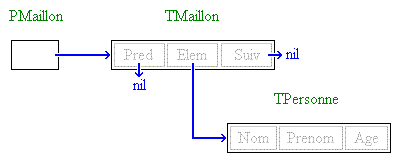
De l'extérieur, seul le type "TListeChaineeTriee" devra être utilisé. Nous allons petit à petit implémenter les opérations de manipulation de ces listes. Commençons par la plus simple : la création d'une liste vide, qui consiste à renvoyer un pointeur vers un record de type _ListeChaineeTriee. On conserve un pointeur vers la fin et un vers le début pour permettre de commencer le parcours de la liste depuis la fin (en utilisant les pointeurs Pred) ou depuis le début (en utilisant les pointeurs Suiv).
function LCTNouvelle: TListeChaineeTriee;
begin
new(result);
result^.Dbt := nil;
result^.Fin := nil;
end;L'opération de test de liste pleine n'a pas de sens ici. On n'implémente donc que celui qui teste si une liste est vide. En pratique, si l'élément est nil, la liste est considérée comme vide, sinon, on teste les deux pointeurs Fin et Dbt et s'ils valent nil tous les deux, la liste est vide.
function LCTVide(Liste: TListeChaineeTriee): boolean;
begin
result := Liste = nil;
if not result then
result := (Liste^.Dbt = nil) and (Liste^.Fin = nil);
end;Avant de passer à la manipulation des éléments, nous allons voir encore une fois à l'aide de schémas comment les listes manipulées ici sont constituées. Nous détaillerons par la suite la procédure d'insertion ou de retrait d'un élément. Voici une liste à un seul élément (Attention, pour faciliter le dessin et sa compréhension, la position de certains champs (Elem et Suiv, Fin et Dbt) seront dorénavant permutées) :
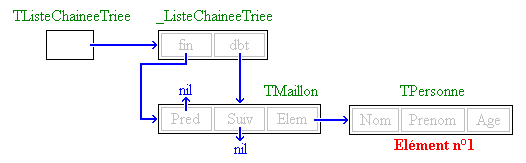
Les étapes indispensables pour construire cette structure seront présentées et expliquées ci-dessous. En attendant, compliquons un peu les choses en ajoutant un élément :
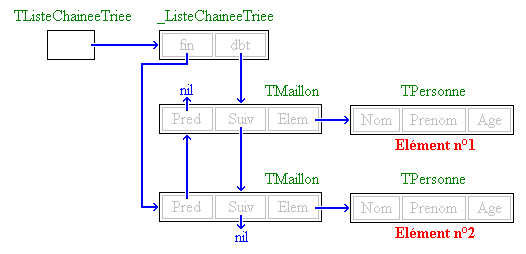
Et, puisque nous y sommes, histoire de vous faire sentir la disposition générale, voici une liste à 3 éléments :
Maintenant que vous voyez à quoi ressemble la structure d'une liste, passons à l'opération d'insertion d'un élément. Plutôt que de commencer en vous lâchant l'insertion avec tri d'une façon brutale, nous allons progresser doucement en insérant au début, à la fin, puis au milieu d'une liste à double chaînage pour bien vous faire comprendre les mécanismes à acquérir. Dans chaque cas, il faut faire attention car le cas où la liste est vide est particulier et doit être traité à part. Voici ce que cela donne (Ne vous effrayez pas) :
function LCTInsereDebut(Liste: TListeChaineeTriee; P: TPersonne): TListeChaineeTriee;
var
Temp: PMaillon;
begin
result := Liste;
if Liste = nil then exit;
// création d'un nouvel élément (maillon)
New(Temp);
New(Temp^.Elem);
// initialisation du nouveau maillon
Temp^.Elem^ := P;
// 2 cas, si la liste est vide ou non
if LCTVide(Liste) then
// initialise une liste à 1 élément (début et fin)
begin
Temp^.Pred := nil;
Temp^.Suiv := nil;
Liste^.Dbt := Temp;
Liste^.Fin := Temp;
end
else
// insertion avant le premier élément
begin
// l'ancien premier élément doit être mis à jour
Liste^.Dbt^.Pred := Temp;
Temp^.Suiv := Liste^.Dbt;
Temp^.Pred := nil;
Liste^.Dbt := Temp;
// Liste^.Fin ne change pas
end;
end;L'insertion doit effectuer plusieurs traitements : le premier consiste à créer le maillon, à créer la mémoire associée au maillon et à recopier les valeurs à mémoriser dans cette mémoire. Une fois le maillon créé, il faut l' « accrocher » en début de liste. Ici, deux cas sont possibles : soit la liste est vide, soit elle ne l'est pas. Ces deux cas nécessitent un traitement à part. Si la liste est vide, Les champs Pred et Suiv sont fixés à nil (cf. illustration de la liste vide ci-dessus) car il n'y a pas d'autre élément dans la liste : le premier élément est aussi le dernier et le premier a toujours son pointeur Pred égal à nil et de même pour le pointeur Suiv du dernier élément. Du fait que l'élément inséré est le premier et le dernier de la liste, les champs Dbt et Fin pointent vers cet élément.
Remarque : il aurait été possible de faire pointer le champ Pred du premier élément sur le dernier, et le champ Suiv du dernier élément sur le premier, ce qui nous aurait donné une liste « circulaire », un peu plus pratique à manipuler, mais j'ai préféré ne pas le faire pour ne pas entraîner de confusion inutile.
Si la liste n'est pas vide, le traitement est un peu plus compliqué : l'élément en
tête de liste avant l'insertion doit être mis à jour pour que son pointeur Pred,
initialement à nil, pointe sur le nouvel élément inséré en tête de liste,
qui le précédera donc immédiatement dans la liste. La première instruction réalise
cela. Le champ Suiv du nouvel élément inséré est fixé à l'ancien premier élément,
encore accessible par "Liste^.Dbt", que l'on modifiera par la suite. Quand au champ
Pred, il est fixé à nil car on insère en début de liste. Enfin, l'insertion
du premier élément est concrétisée par la modification du pointeur "Dbt" de la
liste.
Intéressons-nous à l'ajout en fin de liste. Il ressemble beaucoup à l'ajout en
début de liste, puisque c'est en quelque sorte son « symétrique ». Voici le code
source :
function LCTInsereFin(Liste: TListeChaineeTriee; P: TPersonne): TListeChaineeTriee;
var
Temp: PMaillon;
begin
result := Liste;
if Liste = nil then exit;
// création d'un nouvel élément (maillon)
New(Temp);
New(Temp^.Elem);
// initialisation du nouveau maillon
Temp^.Elem^ := P;
// 2 cas, si la liste est vide ou non
if LCTVide(Liste) then
// initialise une liste à 1 élément (début et fin)
begin
Temp^.Pred := nil;
Temp^.Suiv := nil;
Liste^.Dbt := Temp;
Liste^.Fin := Temp;
end
else
// insertion après le dernier élément
begin
// l'ancien dernier élément doit être mis à jour
Liste^.Fin^.Suiv := Temp;
Temp^.Pred := Liste^.Fin;
Temp^.Suiv := nil;
Liste^.Fin := Temp;
// Liste^.Dbt ne change pas
end;
end;Sans écrire la procédure qui le réalise, analysons l'insertion d'un élément en « milieu » de liste, c'est-à-dire entre deux éléments M1 et M2 déjà présents dans la liste. On appellera pour cela que l'élément inséré M3. Il y a 4 « connections » à réaliser :
- fixer le champ Suiv du maillon M3 à l'adresse de M2 ;
- fixer le champ Prev du maillon M3 à l'adresse de M1 ;
- fixer le champ Suiv du maillon M1 à l'adresse de M3 ;
- fixer le champ Prev du maillon M2 à l'adresse de M3 ;
La procédure d'insertion va donc consister à parcourir la liste depuis son début, et dés que l'endroit où l'élément doit être inséré est déterminé, on réalise l'insertion adéquate. Cette recherche n'a d'ailleurs pas lieu si la liste est initialement vide. Voici le code source ; prenez bien le temps de l'analyser, il n'est pas si long qu'il n'y paraît, car je n'ai pas été avare de commentaires :
function LCTInsere(Liste: TListeChaineeTriee; P: TPersonne): TListeChaineeTriee;
var
Temp, Posi: PMaillon;
begin
result := Liste;
if Liste = nil then exit;
// 1. Création du maillon
New(Temp);
New(Temp^.Elem);
// initialisation du nouveau maillon par le paramètre P
Temp^.Elem^ := P;
// 2. Si la liste est vide, on insère l'élément seul
if LCTVide(Liste) then
// initialise une liste à 1 élément (début et fin)
begin
Temp^.Pred := nil;
Temp^.Suiv := nil;
Liste^.Dbt := Temp;
Liste^.Fin := Temp;
exit;
end;
// 3. On recherche la position d'insertion de l'élément
{ pour cela, on fixe un pointeur au dernier élément de la liste
puis on recule dans la liste jusqu'à obtenir un élément
"intérieur" à celui inséré. 3 cas se présentent alors :
1) on est en début de liste : on sait faire l'ajout
2) on est en fin de liste : idem
3) sinon, on applique la méthode décrite ci-dessus. }
// initialisation du parcours
Posi := Liste^.Fin;
{ tant que l'on peut parcourir et que l'on DOIT parcourir...
(on peut parcourir tant que Posi est non nil et on DOIT
parcourir si la comparaison entre l'élément actuel et l'élément
à insèrer donne le mauvais résultat. }
while (Posi <> nil) and (CompPersonnes(Posi^.Elem, Temp^.Elem) > 0) do
Posi := Posi^.Pred;
// 4. c'est maintenant qu'on peut détecter l'un des trois cas.
// cas 1 : Posi vaut nil, on a parcouru toute la liste
if Posi = nil then
begin
// insertion au début
Liste^.Dbt^.Pred := Temp;
Temp^.Suiv := Liste^.Dbt;
Temp^.Pred := nil;
Liste^.Dbt := Temp;
end
// cas 2 : Posi n'a pas changé, et vaut donc Liste^.Fin.
else if Posi = Liste^.Fin then
begin
// insertion à la fin
Liste^.Fin^.Suiv := Temp;
Temp^.Pred := Liste^.Fin;
Temp^.Suiv := nil;
Liste^.Fin := Temp;
end
// cas 3 : Posi <> Liste^.Fin et <> nil, insertion "normale"
else
begin
{ Posi pointe sur un élément "inférieur", on doit donc
insérer entre Posi et Posi^.Suiv }
Temp^.Suiv := Posi^.Suiv;
Temp^.Pred := Posi;
Posi^.Suiv^.Pred := Temp;
Posi^.Suiv := Temp;
end;
end;
En avant les explications !
Il est à noter ici que l'ordre considéré est le même qu'au paragraphe précédent,
j'ai donc repris la fonction de comparaison. La première partie est très
conventionnelle puisqu'elle se contente de faire quelques tests et initialise le
maillon à insèrer. La section 2 traite le cas où la liste est vide. Dans ce cas,
l'ordre n'a pas d'influence, et on se contente d'initialiser une liste à un
élément, chose que nous avons déjà fait deux fois précédemment. La partie 3 est
plus intéressante car elle effectue la recherche de la position d'insertion du
maillon. On adopte la même technique que pour l'implémentation avec un tableau : on
part du dernier élément et on "remonte" dans la liste jusqu'à obtenir un élément
plus petit que celui à insèrer. Si l'élément est plus grand que le dernier de la
liste, le parcours s'arrètera avant de commencer car la première comparaison
"cassera" la boucle. Si l'élément est plus petit que tous ceux présents dans la
liste, c'est la condition Posi <> nil qui nous permettra d'arrêter
la boucle lorsque l'on sera arrivé au début de la liste et qu'il sera devenu
impossible de continuer la "remontée", faute d'éléments. Le troisième cas,
intermédiaire, est lorsqu'un élément parmi ceux de la liste est plus petit que celui
inséré. Il y a alors arrèt de la boucle et Posi pointe sur cet élément.
L'étape 4 traite ces trois cas à part. La distinction des cas se fait en examinant
la valeur de Posi. Si l'élément est plus grand que le dernier de la liste, Posi n'a
jamais été modifié et vaut donc toujours Liste^.Fin. Si Posi vaut nil, c'est
qu'on est dans le second cas, à savoir que le nouveau maillon est plus petit que
tous ceux de la liste, ce qui force son insertion en début de liste. Le troisième
et dernier cas utilise la valeur de Posi qu'on sait utilisable puisqu'elle ne vaut
pas nil. On effectue donc l'insertion entre l'élément pointé par Posi et
celui pointé par Posi^.Suiv. Les deux premières méthodes d'insertion (début et fin
de liste) ont déjà été vues, intéressons-nous donc plutôt à la troisième.
On commencer par fixer les champs Suiv et Pred du nouveau maillon. Comme on doit
insèrer entre l'élément pointé par Posi et Posi^.Suiv, on affecte ces valeurs
respectivement à Pred et à Suiv. Les deux autres instructions ont pour but de faire
pointer le champ Suiv de l'élément pointé par Posi vers le nouveau maillon, et de
même pour le champ Pred de l'élément pointé par Posi^.Suiv.
La suppression d'un élément fonctionne sur le même principe que pour
l'implémentation avec un tableau : on donne le numéro d'un élément et si cet
élément existe, il est retiré de la liste et détruit. La suppression est donc assez
proche de l'insertion. Après quelques vérifications, une recherche est lancée sous
la forme d'un parcours linéaire de la liste, afin de localiser l'élément. Si
l'élément n'a pas été trouvé, la fonction se termine. Sinon, on doit d'une part
retirer les références à cet élément dans la liste, ce qui se fait de 3 manières
différentes suivant que l'élément est le premier, le dernier, ou un autre, et
d'autre part supprimer l'élément en libérant la mémoire.
function LCTSupprIdx(Liste: TListeChaineeTriee; index: integer): TListeChaineeTriee;
var
indx: integer;
Posi: PMaillon;
begin
result := Liste;
if Liste = nil then exit;
if index < 0 then exit;
if LCTVide(Liste) then exit;
// initialisation
indx := 0;
Posi := Liste^.Dbt;
// parcours pour tenter d'obtenir l'élément
while (Posi <> nil) and (indx < index) do
begin
inc(indx);
Posi := Posi^.Suiv;
end;
// l'élément n°index existe pas, on quitte
if Posi = nil then exit;
{ on supprime dans un premier temps les références à Posi
dans la liste }
if Posi = Liste^.Dbt then
begin
Liste^.Dbt := Posi^.Suiv;
{ suppression de la référence dans l'élément suivant :
attention, celui-ci n'existe pas toujours }
if Posi^.Suiv <> nil then
Posi^.Suiv^.Pred := nil
else
Liste^.Fin := nil;
end
else if Posi = Liste^.Fin then
begin
Liste^.Fin := Posi^.Pred;
{ suppression de la référence dans l'élément précédent :
attention, celui-ci n'existe pas toujours }
if Posi^.Pred <> nil then
Posi^.Pred^.Suiv := nil
else
Liste^.Dbt := nil;
end
else
begin
Posi^.Pred^.Suiv := Posi^.Suiv;
Posi^.Suiv^.Pred := Posi^.Pred;
end;
// maintenant, on supprime le maillon
Dispose(Posi^.Elem);
Dispose(Posi);
end;
Quelques explications encore : dans le cas où l'élément supprimé est le premier ou
le dernier, il faut non seulement mettre à jour respectivement le champ Dbt ou le
champ Fin, mais faire attention à un cas particulier : si l'élément supprimé est le
dernier (ce qui ne peut pas se produire si l'élément est au "milieu" de la liste),
il faudra en plus fixer respectivement le champ Fin ou le champ Dbt de la liste à
nil, afin de respecter notre convention pour la liste vide, à savoir Dbt =
Fin = nil.
Il est maintenant temps de passer à un exercice. Vous allez programmer certaines
des opérations restantes. Pour cela, vous pouvez vous aider de l'unité lst_dbl_ch.pas
qui comporte tout ce que nous avons fait jusqu'à présent. Vous pourrez ainsi
incorporer le code de cette unité dans un projet (Menu Projet, choix "Ajouter au
projet...") et la complèter.
Exercice 1 : (voir la
solution
et les commentaires)
A l'aide de l'unité téléchargeable ci-dessus, écrivez le code source des deux
opérations et de la procédure d'affichage décrits ci-dessous :
- LCTNbElem : fonction retournant le nombre d'éléments dans une liste.
- LCTDetruire : procédure libèrant toute la mémoire associée aux personnes, aux maillons et à la liste.
- AfficheListe : procédure affichant le contenu d'une liste dans une "Sortie". (voir les commentaires pour chaque fonction/procédure dans l'unité téléchargeable)
Une fois cet exercice réalisé, vous pouvez lire la correction proposée et passer à
la suite où une unité complète intégrée dans un projet exemple est disponible.
En adaptant le projet utilisé pour tester les listes implémentées dans un tableau,
on peut facilement tester les listes à double chaînage. Cette application a déjà
été décrite plusieurs fois dans ce chapitre (elle marche presque toujours sur le
même principe. Les modifications à apporter concernant les noms des opérations à
utiliser, le type de la liste Lst, et consiste à remplacer l'unité implémentant une
liste par un tableau par celle que vous venez de complèter si vous avez fait
l'exercice précédent. Vous pouvez télécharger le
projet terminé.
Voilà pour les listes triées à l'insertion. les deux méthodes présentées ici ont eu
non seulement pour but de vous démontrer une fois de plus l'abstraction de la
structure des données qui peut être réalisée dans une application (presque pas de
changements dans l'application de tests alors que le type des données a
complètement changé entre la représentation par un tableau et la représentation
chaînée), mais également de vous familiariser avec ce concept trop souvent
considéré comme difficile que sont les listes doublement chaînées. Je me suis
justement attaché ici à donner des explications et des schémas permettant leur
compréhension plutôt que d'essayer d'optimiser inutilement le code source qui les
manipule.
Dans la section suivante, nous allons abandonner le tri à l'insertion pour le tri à
la demande. C'est une approche différente qui permet notamment différents ordres de
tri sur une même liste. C'est également l'approche adoptée pour les objets TList et
TStringList fournis par Delphi.
XV-D-5. Implémentation permettant différents tris▲
XV-D-5-a. Présentation▲
Lorsqu'on ne sait pas exactement quel ordre de tri sera nécessaire sur une liste,
ou encore si on doit pouvoir choisir entre plusieurs méthodes de tri pour une
seule liste, ou tout simplement si on ne souhaite pas du tout une liste triée, il
est intéressant de séparer les deux concepts : la manipulation des entrées de la
liste (ajout, insertion (ces deux notions étaient confondues pour les listes
triées, elle ne vont plus l'être ici), déplacement (à noter que le déplacement
était auparavant impossible car l'ordre de tri fixait la place des éléments),
suppression) d'un coté, et le tri d'un autre coté. Ainsi, il sera possible de
paramètrer un tri et de le lancer seulement lorsque ce sera nécessaire. Cette
approche a cependant un inconvénient puisque le tri peut avoir à être relancé à
chaque ajout/insertion d'un élément, ce qui peut ralentir les traitements.
Commençons comme d'habitude par formaliser un peu la notion de liste non triée :
- Création d'une nouvelle liste vide
paramètres : (aucun)
résultat : liste vide - Destruction d'une liste
paramètres : une liste
résultat : (aucun) - Insertion d'un élément
paramètres : une liste, un élément du type stocké dans la liste, un index de position
résultat : une liste contenant l'élément inséré à la position demandée ou à défaut en fin de liste - Ajout d'un élément
paramètres : une liste, un élément du type stocké dans la liste
résultat : une liste contenant l'élément en fin de liste - Suppression d'un élément
paramètres : une liste, un élément du type stocké dans la liste
résultat : une liste où l'élément transmis a été supprimé
(Note : on se permettra souvent, dans la pratique de remplacer l'élément par son index) - Nombre d'éléments
paramètres : une liste
résultat : un entier indiquant le nombre d'éléments dans la liste - Accès à un élément
paramètres : une liste, un entier
résultat : sous réserve de validité de l'entier, l'élément dont le numéro est transmis - Tri de la liste
paramètres : une liste, un ordre
résultat : une liste triée en fonction de l'ordre transmis
Comme d'habitude, nous ajouterons une procédure d'affichage du contenu d'une liste
écrivant dans une Sortie de type TStrings. Quelques précisions sont à apporter sur
les opérations ci-dessus. L'insertion consiste à placer un élément à la position
spécifiée, en décalant si besoin les éléments suivants. Etant donné que les n
éléments d'une liste seront numérotés de 0 à n-1, les valeurs autorisées iront de
0 à n, n signifiant l'ajout standard, c'est-à-dire en fin de liste. Bien qu'il
soit normalement préférable de programmer une suppression ayant pour paramètre
l'élément à supprimer, il est beaucoup plus simple et plus efficace, dans la
plupart des cas, d'implémenter une suppression s'appliquant sur l'élément dont
l'index est transmis.
Vous êtes peut-être intrigué(e) par le second paramètre donné à l'opération de
tri. En effet, si vous êtes un peu dans les maths, l'ordre transmis doit
constituer une relation d'ordre total sur l'ensemble des éléments stockable dans
la liste. Si vous n'êtes pas dans les maths, sachez simplement que ce paramètre va
nous permettre de décider pour deux éléments quelconques, lequel est le "plus
petit" et lequel est le "plus grand". En pratique, le paramètre transmis à la
fonction sera d'un type encore inconnu de vous, dont nous allons parler tout de
suite.
XV-D-5-b. Paramètres fonctionnels▲
Nous allons faire un petit détour par ce qui s'appelle les paramètres
fonctionnels. Par ce terme un peu trompeur de "paramètre fonctionnel", on désigne
en fait un paramètre d'une fonction ou d'une procédure dont le type est lui-même
une fonction (les paramètres procéduraux permettent la même chose avec les
procédures). Il est ainsi possible de transmettre le nom d'une fonction existante
comme paramètre d'une autre fonction/procédure. L'utilité de ce genre de procédé
n'est pas à démontrer si vous avez pratiqué des langages tels que le C ou le C++.
Sinon, sachez simplement que ce genre de paramètre sera d'une grande utilité pour
spécifier l'ordre d'un tri. J'expliquerai pourquoi et comment en temps voulu. Mais
revenons-en à nos moutons.
Un paramètre fonctionnel doit être typé par un type "fonctionnel" défini
manuellement dans un bloc type. Voici un exemple qui va servir de base à la
définition plus générale :
type
TFuncParam = function (S: string): integer;Comme vous pouvez le constater, le bloc ci-dessus définit un nouveau type fonctionnel appelé TFuncParam. La morphologie de la définition de ce type est nouvelle. Elle correspond en fait à la ligne de déclaration d'une fonction privée du nom de la fonction. Ainsi, lorsqu'on définit une fonction
function Longueur(S: string): integer;son type est :
function (S: string): integer;
ce qui fait que notre fonction Longueur est de type "TFuncParam".
Une fois un type fonctionnel défini, il peut être employé comme type d'un ou de
plusieurs paramètres d'une fonction/procédure. Ainsi, voici le squelette d'une
fonction recevant un paramètre fonctionnel et un autre de type chaîne :
function Traite(S: string; FonctionTraitement: TFuncParam): integer;
begin
end;Un appel possible de cette fonction peut alors se faire en donnant pour "valeur" du paramètre le nom d'une fonction du type fonctionnel demandé. Ainsi, on pourrait appeler "Traite" de la manière suivante :
Traite('Bonjour !', Longueur);car "Longueur" est bien du type fonctionnel défini pour le second paramètre. A l'intérieure d'une fonction/procédure acceptant un paramètre fonctionnel, le paramètre doit être considéré comme une fonction à part entière, dont la définition est donnée par son type (paramètres, résultat) que l'on peut appeler comme n'importe quelle fonction. Ainsi, voici la fonction "Traite" complétée pour faire appel à son paramètre fonctionnel :
function Traite(S: string; FonctionTraitement: TFuncParam): integer;
begin
result := FonctionTraitement(S);
end;
Ainsi, si on appelle Traite comme dans l'exemple ci-dessus (avec 'Bonjour !' et Longueur), le résultat sera 9, car la
fonction Longueur sera appelée avec la chaîne 'Bonjour
!' en paramètre et le résultat sera retourné par "Traite".
Les paramètres fonctionnels (et leurs alter-ego procéduraux) sont à ma
connaissance assez rarement utilisés, malgré la souplesse de programmation qu'ils
peuvent procurer. Nous nous en servirons d'ailleurs uniquement pour les tris.
XV-D-5-c. Implémentation du tri à la demande▲
Concrètement, les paramètres fonctionnels vont nous permettre de généraliser
l'emploi d'une fonction de comparaison telle que CompPersonnes. Au lieu d'appeler
une procédure nommée explicitement dans le code, nous allons utiliser un paramètre
fonctionnel que devra fournir le programmeur utilisant la liste. Ainsi, il sera
libre de définir ses fonctions de comparaison permettant d'obtenir des tri
particuliers, et d'appeler ensuite l'opération de tri en donnant en paramètre
l'une de ces fonctions de comparaison.
Nous allons reprendre ici l'implémentation par double chaînage pour nos listes.
Les éléments manipulés seront donc de type TPersonne. Voici la déclaration du type
fonctionnel qui nous servira à spécifier une fonction de comparaison. On demande
toujours deux paramètres du type manipulé dans la liste et le résultat est
toujours un entier négatif, positif ou nul si le premier élément est
respectivement plus petit, plus grand ou égal au second :
TCompareFunction = function(P1, P2: PPersonne): integer;
Toutes les opérations sont identiques, sauf l'ajout qui se scinde en deux
opérations distinctes : l'ajout ou l'insertion, ainsi que l'opération de tri qui
est à créer entièrement.
En ce qui concerne l'ajout, ce n'est pas très compliqué puisque c'est un ajout en
fin de liste. On retrouve donc un code source identique à celui de LCTInsereFin.
Voici :
function LPAjout(Liste: TListePersonnes; P: TPersonne): TListePersonnes;
var
Temp: PMaillon;
begin
Result := Liste;
if Liste = nil then exit;
// création d'un nouvel élément (maillon)
New(Temp);
New(Temp^.Elem);
// initialisation du nouveau maillon
Temp^.Elem^ := P;
// 2 cas, si la liste est vide ou non
if LPVide(Liste) then
// initialise une liste à 1 élément (début et fin)
begin
Temp^.Pred := nil;
Temp^.Suiv := nil;
Liste^.Dbt := Temp;
Liste^.Fin := Temp;
end
else
// insertion après le dernier élément
begin
// l'ancien dernier élément doit être mis à jour
Liste^.Fin^.Suiv := Temp;
Temp^.Pred := Liste^.Fin;
Temp^.Suiv := nil;
Liste^.Fin := Temp;
// Liste^.Dbt ne change pas
end;
end;Pour ce qui concerne l'insertion, c'est un peu plus compliqué, car il y a divers cas. La première étape consistera à vérifier la validité de la liste et de l'index transmis. Ensuite, un premier cas particulier concerne une liste vide. Quel que soit l'index donné, l'élément sera inséré en tant qu'élément unique. Un second cas particulier est alors le cas où l'index vaut 0 : dans ce cas on effectue une insertion en début de liste. Si aucun de ces deux cas ne se présente, l'élément ne sera pas inséré en début de liste, et donc un élément le précédera. Partant de cela, on recherche l'élément précédent en parocurant la liste jusqu'à arriver à l'élément en question ou à la fin de la liste. Si c'est ce dernier cas qui se produit (index trop grand) l'élément est inséré en fin de liste. Sinon il y a encore deux cas : soit l'élément trouvé est le dernier de la liste et l'insertion se fait en fin de liste, soit ce n'est pas le dernier et l'insertion se fait entre l'élément trouvé et son "suivant" (champ Suiv). je ne reviendrai pas sur les détails techniques de chaque cas d'insertion (liste vide, en début, en fin, au milieu) car je l'ai déjà fait. Voici le code source :
function LPInsere(Liste: TListePersonnes; P: TPersonne; index: integer): TListePersonnes;
var
indxPosi: integer;
Temp, Posi: PMaillon;
begin
Result := Liste;
if Liste = nil then exit;
if index < 0 then exit;
// 1. Création du maillon
New(Temp);
New(Temp^.Elem);
// initialisation du nouveau maillon par le paramètre P
Temp^.Elem^ := P;
// 2. Si la liste est vide, on insère l'élément seul
if LPVide(Liste) then
// initialise une liste à 1 élément (début et fin)
begin
Temp^.Pred := nil;
Temp^.Suiv := nil;
Liste^.Dbt := Temp;
Liste^.Fin := Temp;
exit;
end;
// 3. Cas particulier : si index = 0, insertion en tête
if index = 0 then
begin
Liste^.Dbt^.Pred := Temp;
Temp^.Suiv := Liste^.Dbt;
Temp^.Pred := nil;
Liste^.Dbt := Temp;
exit;
end;
// 4. Recherche de l'élément "précédent", c'est-à-dire de l'élément
// qui précédera l'élément inséré après insertion.
indxPosi := 1;
Posi := Liste^.Dbt;
while (Posi <> nil) and (indxPosi < index) do
begin
inc(indxPosi);
Posi := Posi^.Suiv;
end;
{ 3 cas sont possibles :
- Posi pointe sur l'élément "précédent", comme souhaité, ce qui
donne deux sous cas :
- Posi pointe sur le dernier élément de la liste, ce qui donne
une insertion à la fin
- Dans le cas contraire, c'est une insertion classique entre deux éléments.
- Posi vaut nil, ce qui donne une insertion en fin de liste. }
// cas 1 : Posi est non nil et est différent de Liste^.Fin
if (Posi <> nil) and (Posi <> Liste^.Fin) then
begin
Temp^.Suiv := Posi^.Suiv;
Temp^.Pred := Posi;
Posi^.Suiv^.Pred := Temp;
Posi^.Suiv := Temp;
end
else
begin
// insertion à la fin
Liste^.Fin^.Suiv := Temp;
Temp^.Pred := Liste^.Fin;
Temp^.Suiv := nil;
Liste^.Fin := Temp;
end;
end;Venons-en à la procédure de tri. Nous allons avoir besoin d'un accès à un maillon par son numéro. Le mieux est de créer une opération "interne" (non accessible depuis l'extérieur) qui permettra ce genre d'accès. Voici son code source :
function LPGetMaillon(Liste: TListePersonnes; index: integer): PMaillon;
var
indx: integer;
begin
indx := 0;
Result := Liste^.Dbt;
while indx < index do
begin
Result := Result^.Suiv;
inc(indx);
end;
end;Etant donné que cette opération est interne à l'unité, elle n'effectue aucun test. Elle se contente d'utiliser un compteur et un élément pour parcourir la liste depuis son début. Lorsque le compteur est arrivé à la valeur désirée, l'élément en cours est lui-même le maillon désiré, que l'on retourne. Quant à la procédure de tri, elle accepte deux paramètres : une liste et une fonction de type "TCompareFunction". L'algorithme retenu pour effectuer le tri est le "Shell Sort" décrit dans la section consacrée aux tris. la fonction de comparaison fournie est utilisae pour comparer deux éléments lorsque c'est nécessaire, et le reste est simplement adapté à la structure triée. Referrez-vous au code source téléchargeable dans la section sur les tris pour avoir une version plus simple du Shell Sort. Voici le code source de la fonction de tri :
function LPTrieListe(Liste: TListePersonnes; Compare: TCompareFunction): TListePersonnes;
// l'algorithme retenu est celui du Shell Sort
// implémentation de ShellSort inspirée de "Le Language C - Norme ANSI" (ed. DUNOD)
var
ecart, i, j, N: Integer;
Mj, Mje: PMaillon;
tmpPers: PPersonne;
begin
result := Liste;
N := LPNbElem(Liste);
ecart := N div 2;
// écart détermine l'écart entre les cases comparées entre elles
while ecart > 0 do
begin
{ parcours des éléments du tableau (tous seront
parcourus puisque ecart s'annulera) }
for i := ecart to N - 1 do
begin
j := i - ecart;
// comparaisons et permutations d'éléments
Mj := LPGetMaillon(Liste, j);
Mje := LPGetMaillon(Liste, j + ecart);
while (j >= 0) and (Compare (Mj^.Elem, Mje^.Elem) > 0) do
begin
// permutation des personnes et non des maillons
tmpPers := Mj^.Elem;
Mj^.Elem := Mje^.Elem;
Mje^.Elem := tmpPers;
// calcul de la nouvelle valeur de j
j := j - ecart;
{ et obtention des nouveaux maillons }
Mj := LPGetMaillon(Liste, j);
Mje := LPGetMaillon(Liste, j + ecart);
end;
end;
// écart diminie progressivement jusqu'à 0
ecart := ecart div 2;
end;
end;
Cette implémentation permet d'appliquer n'importe quel tri à une liste. Il suffit
de créer une fonction de comparaison permettant d'obtenir le tri souhaité et le
simple fait d'appeler l'opération de tri sur la liste effectue le tri dans l'ordre
prévu. Ceci permet de se consacrer à la manière dont l'on veut trier et de ne pas
s'embêter dans les détails d'implémentation de l'algorithme de tri.
Je suis conscient de vous avior noyé dans baeucoup trop de lignes de code. Je m'en
excuse... Voici pour enfoncer le clou l'application permettant de tester les
listes triées à la demande : lsttriables.zip.
Ceci termine la (trop longue) section consacrée aux listes. Les deux dernières
sections de ce (trop long, également) chapitre sont consacrées aux structures non
plus « linéaires » comme celles que nous venons d'étudier, mais arborescentes.
XV-E. Arbres▲
Certaines données informatiques ne peuvent pas (facilement) être représentées par
des structures linéaires comme celles présentées dans les sections précédentes de
ce chapitre. Ces données doivent être représentées par une structure mettant en
valeur leur type de relation, arborescent ou parfois "graphique". Les structures
d'arbres permettent ainsi de représenter des structures en relation de type
arborescent, comme des répertoires d'un disque dur par exemple. Le cas des
relation de type "graphique" ne nous intéresse pas ici car il est plus complexe
et s'appuie en informatique sur la théorie des graphes, sujet haut en couleur et
beaucoup trop vaste et trop long pour être abordé ici.
Par arbre, on entend en informatique une structure où chaque élément peut avoir
plusieurs sous-éléments, mais où chaque élément ne peut avoir qu'un sur-élément.
Voici un exemple d'arbre :
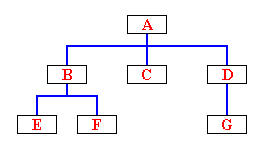
Je ne parlerais pas ici de la signification d'un tel arbre, tout ce qui m'intéresse,
c'est la représentation arborescente des éléments. Il serait certes possible de
représenter cette structure dans une liste, mais ce serait un peu pénible à élaborer
et à utiliser. Il serait plus intéressant d'élaborer des structures informatiques
permettant une gestion de l'arborescence au niveau du code Pascal. Encore une fois,
ceci se fait par l'utilisation intensive des pointeurs.
Avant de passer à la définition de structures Pascal, je vais me permettre de vous
infliger quelques définitions un peu formelles. Un arbre est composé de noeuds et de
branches. Une branche relie deux noeuds et chaque noeud possède une étiquette. Les
informations à stocker dans l'arbre sont stockées exclusivement dans les étiquettes
des noeuds. Une branche permet de relier deux noeuds. L'un de ces deux noeuds est
appelé noeud parent et l'autre noeud enfant (appelé aussi fils). Un noeud parent
peut avoir 0, un ou plus de noeuds enfants. Un noeud enfant a, sauf exception d'un
seul noeud dans l'arbre, un et un seul noeud parent. Tout arbre non vide (contenant
un noeud) possède un et un seul noeud ne possèdant pas de noeud parent. Ce noeud est
nommé racine de l'arbre.
Un arbre peut contenir 0, 1 ou plus de noeuds. Les noeuds ne possédant pas de noeuds
enfant sont appelés feuilles de l'arbre (que c'est original, tout ça !). A priori,
pour un noeud qui n'est pas une feuille, il n'y a pas d'ordre dans l'ensemble de ses
sous-noeuds, même si la représentation physique des données introduit souvent un
ordre « artificiel ». Un sous-arbre engendré par un noeud est l'arbre dont la
racine est ce noeud (tous les noeuds qui ne sont ni le noeud ni un de ses
"descendants" sont exclus de ce sous-arbre). Par exemple, dans l'exemple ci-dessus,
le sous-arbre engendré par A est l'arbre entier, tandis que le sous-arbre engendré
par B est l'arbre dont B est la racine (les noeuds A, C, D et G sont exclus de cet
arbre).
L'implémentation de types de données arborescents fait une utilisation intensive des
pointeurs. Assurez-vous avant de continuer à lire ce qui suit que vous avez bien
compris le concept de liste chaînée car il va être ici employé. Au niveau Pascal, on
va créer un type TNoeud qui contiendra deux champs. Le premier sera l'étiquette du
noeud, qui sera en pratique un pointeur vers une autre structure contenant les
vraies données associées au noeud (un pointeur de type PPersonne vers un élément de
type TPersonne pour l'exemple). Le second champ sera une liste chaînée, simplement
ou doublement, suivant les besoins (dans notre cas, elle le sera simplement, pour
simplifier). Les éléments stockés par cette liste chaînée seront des pointeurs vers
des noeuds fils du noeud en cours. Le type Arbre sera défini comme étant un pointeur
vers un noeud qui sera le noeud racine. Lorsque l'arbre sera vide, ce pointeur sera
nil. Voici quelques déclarations que je vais expliquer plus en détail
ci-dessous :
type
TFonction = (fcAucune, fcPDG, fcDirecteur, fcIngenieur, fcSecretaire);
PElem = ^TPersonne;
TPersonne = record
Nom,
Prenom: string;
Age: integer;
Fonction: TFonction;
end;
PNoeud = ^TNoeud;
PListeNoeud = ^TListeNoeud;
TNoeud = record
Elem: PElem;
Fils: PListeNoeud;
end;
TListeNoeud = record
Noeud: PNoeud;
Suiv: PListeNoeud;
end;
Arbre = PNoeud;
L'élément de type TPersonne servira à stocker les infos sur une personne. Chaque
personne constituera l' « étiquette » d'un noeud. Le type PPersonne permettra
d'utiliser des pointeurs sur ces éléments. Le type TNoeud est la structure centrale
qui nous permettra de gèrer les arbres : il possède, comme je l'ai annoncé plus
haut, deux champs. Le premier est un pointeur vers l'étiquette, de type TPersonne
dans notre cas. Le second est un élément de type PListeNoeud qui est le début d'une
liste simplement chaînée de maillons dont chacun pointe sur un autre noeud. Cette
liste chaînée permettra de mémoriser les noeuds « enfant » du noeud en cours (chaque
noeud possèdera un exemplaire propre de cette liste, qui sera simplement nil
si le noeud n'a pas de fils (c'est une feuille).
Pour que vous voyez mieux à quoi ressemblera la structure de données utilisant ces
diverses structures de base, j'ai transcrit le petit arbre présenté plus haut en un
schémas utilisant les structures que nous venons de découvrir. Prenez le temps
d'étudier et de comprendre ce schémas en repérant notamment le découpage logique en
zones, où chaque « zone » sert à stocker un élément de l'arbre :
Comme vous pouvez le constater, la représentation de ce genre de structure de
données est assez délicate, mais est d'une grande puissance car elle permet de
représenter tout arbre de personnes, ce qui est précisément le but recherché.
Arrivé à ce point, je pourrais vous donner et expliquer les opérations destinées à
manipuler un tel arbre. Ce serait, vous vous en doutez, passionnant et très long.
Cependant, je vais me permettre de ne pas le faire, tout en vous promettant d'y
revenir plus tard. En effet, lorsque vous aurez découvert la création d'objets dans
un prochain chapitre, vous constaterez qu'il est nettement plus intéressant de
construire un ensemble de classes manipulant un tel arbre général. Ceci nous
permettra de plus de généraliser ce genre d'arbre en permettant à priori le stockage
de n'importe quel élément dans l'arbre. Je consacrerai toute une partie du chapitre
sur la création d'objets à implémenter cette structure d'arbre fort utile.
Remarque : je sais que je m'expose à de vives critiques en faisant ce choix. Si vous ne partagez pas mon opinion, ou si vous voulez donner votre avis, contactez-moi et nous en discuterons : je suis ouvert à la discussion.
En attendant, la dernière partie de ce chapitre va parler d'un cas particulier d'arbres : les arbres binaires.
XV-F. Arbres binaires▲
Note : Je ne donne ici qu'un bref aperçu des notions attachées aux arbres binaires. En effet, le sujet est extrêmement vaste et ce chapitre est avant tout destiné à vous aider à modèliser vos structures de données en Pascal et à les manipuler, et non pas à vous inculquer des notions qui n'ont pas leur place ici.
Les arbres binaires sont des cas particuliers d'arbres. Un arbre binaire est soit un arbre vide (aucun noeud), soit l'association d'un noeud et de deux arbres binaires nommés respectivement "sous-arbre gauche" et "sous-arbre droit". La racine de chacun de ces arbres, si elle existe (car chaque arbre, gauche ou droite, peut être vide) est nommée respectivement "fils gauche" et "fils droit". Voici les représentations formelles d'un arbre binaire vide ou non vide :
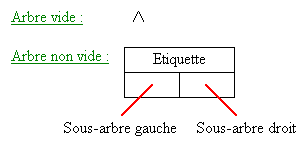
Habituellement, lorsqu'on fait une représentation d'un arbre binaire, on ne fait pas figurer les sous-arbres vides, (ce qui peut avoir pour conséquence de croire qu'un noeud n'a qu'un sous-noeud (voir-ci-dessous), ce qui est impossible, dans l'absolu). De plus, on évite la notation un peu trop formelle présentée ci-dessus, qui a cependant l'avantage d'être plus explicite. Ainsi, la représentation de l'arbre binaire suivant, quelque peu encombrante :
... sera avantageusement remplacée par la représentation suivante, nettement plus sympathique mais à prendre avec plus de précautions, car masquant tous les sous-arbres vides :
Au niveau informatique, un arbre binaire est bien plus maniable et simple à
représenter qu'un arbre général : ayant seulement deux fils, il n'y a pas besoin
d'utiliser une liste chaînée de fils pour chaque noeud. A la place, deux champs «
Fils Gauche » et « FilsDroit » feront parfaitement l'affaire (leur représentation
devra permettre de représenter le vide ou un arbre binaire, ce qui orientera
notre choix vers les pointeurs, encore une fois). Contrairement aux structures
linéaires telles que les piles, files et listes, il est utopique de vouloir
garantir l'indépendance entre implémentation et utilisation de telles structures
(seule une modélisation avec des objets permettrait de garantir ce genre
d'indépendance, mais c'est une autre histoire !). Nous ne parlerons donc pas ici
d'opérations mais seulement de procédures et de fonctions permettant le
traitement d'arbres binaires. Rassurez-vous, dans la plupart des cas, ce sera
amplement suffisant, mis à part pour les perfectionnistes qui trouveront de toute
manière toujours quelque chose à repprocher à une modélisation.
Un arbre binaire sera donc représenté par un pointeur vers le noeud racine de
l'arbre binaire (si l'arbre est non vide). Dans le cas d'un arbre vide, le pointeur
sera nil). Chaque noeud sera constitué par un enregistrement comportant trois
champs : le premier sera l'étiquette, qui en pratique pourra être un pointeur vers
une autre structure ou plus simplement une variable ou un enregistrement. Les deux
autres champs seront deux pointeurs vers le sous-arbre gauche et droite. Voici ce
que cela donne en prenant une chaîne comme étiquette :
type
PNoeud = ^TNoeud;
TNoeud = record
Etiq: TEtiq;
FG,
FD: PNoeud;
end;
TEtiq = string;
TArbin = PNoeud;
Le champ "Etiq" stockera l'étiquette du noeud, tandis que les champs "FG" et "FD"
pointeront respectivement sur les sous-arbres gauche et droite (s'ils ne sont pas
vides).
je ne parlerai ici que de la construction, de l'utilisation et de la destruction
d'un arbre binaire. Les modifications de structure telles que les échanges de
sous-arbres, les rotations (pour l'équilibrage d'arbres binaires) ne seront pas
traitées ici, pour ne pas noyer la cible privilégiée de ce guide - les débutants -
dans trop de détails. Il y a principalement deux méthodes pour construire un arbre
binaire. Soit on commence par la racine, en créant ensuite chacun des deux
sous-arbres, et ainsi de suite jusqu'aux feuilles, soit on commence par les
feuilles, et on les rassemble progressivement par un « enracinement » (un sous-arbre
gauche, un sous-arbre droit et une étiquette en entrée, un arbre binaire comprenant
ces trois éléments en sortie) jusqu'à obtenir l'arbre binaire désiré. Cette
construction ne pose en général aucun problème.
La première méthode se fera créant un noeud, et en modifiant les champs de
l'enregistrement pointé pour créer les deux sous-arbres. La seconde méthode est en
général plus élégante, quoique moins naturelle. Elle permet d'utiliser une fonction
"Enraciner" qui permet de créer un arbre binaire à partir d'une étiquette et de deux
arbres binaires. Pour créer une feuille, il suffira de fournir deux sous-arbres
vides.
C'est cette dernière méthode que je vais décrire, car c'est celle qui vous servira
le plus souvent, et entre autres pour le mini-projet proposé en fin de chapitre.
Nous allons donc simplement écrire deux fonctions. La première sera chargée de
donner un arbre vide, et la seconde effectuera l'enracinemetn de deux arbres dans
une racine commune. Voici le code source, assez simple, de ces deux fonctions :
function ABVide: TArbin;
begin
result := nil;
end;
function Enraciner(E: TEtiq; G, D: TArbin): TArbin;
begin
new(result);
result^.Etiq := E;
result^.FG := G;
result^.FD := D;
end;
La première fonction ne mérite aucune explication. La seconde alloue un espace
mémoire pour stocker un noeud de l'arbre (la racine de l'arbre qui est créé par
l'enracinement). L'étiquette et les deux sous-arbres sont ensuite référencés dans
cet espace mémoire, ce qui crée un arbre dont la racine porte l'étiquette transmise
et dont les deux sous-arbres gauche et droite sont ceux transmis.
Si nous voulons construire l'arbre binaire donné en exemple plus haut, il nous
faudra deux variables temporaires recevant les branches. Soient X et Y ces deux
variables. Le type de ces variables sera bien entendu TArbin. Voici le début de ce
qu'il faudra faire :
X := Enraciner('C', ABVide, ABVide);
Y := Enraciner('D', ABVide, ABVide);Ceci permet de créer les deux "feuilles" C et D (chacune de ces deux "feuilles" est en fait un arbre binaire dont les deux sous-arbres sont vides). Pour créer le branche de racine B et contenant les deux feuilles C et D, on utilise les deux éléments juste construits. Le résultat est affecté à X (on pourrait utiliser une troisième variable Z, mais ce serait inutile puisqu'on n'a plus besoin d'avoir accès à la feuille C. Voici l'instruction qui effectue cet enracinement :
X := Enraciner('B', X, Y);On ne peut pas tout de suite continuer à remonter dans l'arbre, car la partie droite n'existe pas encore. On commence donc par la créer. Pour cela, on ne doit pas toucher à la variable X qui conserve pour l'instant le sous-arbre gauche de l'arbre final. Voici les instructions qui construisent la partie droite :
Y := Enraciner('F', ABVide, ABVide);
Y := Enraciner('E', ABVide, Y);Vous notez que dans la seconde instruction, le sous-arbre gauche étant vide, on fait à nouveau appel à ABVide. Voici enfin l'enracinement qui complète l'arbre. Le résultat est à nouveau stocké dans X :
X := Enraciner('A', X, Y);
Voilà pour ce qui est de la construction. Comme vous pouvez le constater, ce n'est
pas très compliqué, à condition évidemment que les données se prêtent à ce genre
de construction. Pour ce qui est de la destruction d'un arbre, la procédure qui
réalise cela a quelque chose de particulier car elle peut être de deux choses
l'une : très simple ou très compliquée ! Je m'explique : on peut programmer cette
suppression de manière itérative, ou bien de manière récursive. La manière
itérative utilise des boucles pour s'exécuter et parcourir tout l'arbre. Elle est
plus rapide et consomme moins de mémoire. C'est plus compliqué qu'il n'y paraît
car pour parcourir l'arbre, on doit mémoriser la branche en cours, pour aller
supprimer son sous-arbre gauche (ce faisait, on perd la référence à la branche
parent), puis son sous-arbre droit (mais comment va-t-on faire puisqu'on a perdu
la branche parente ???). Bref, c'est tout-à-fait faisable, mais en utilisant une
astuce : il faut utiliser une pile. C'est compliqué et il est plus intéressant
de vous présenter la méthode récusrive (mais rien ne vous empêche de la programmer
à titre d'exercice sur les piles et les arbres binaires).
je n'ai pas encore eu l'occasion de parler des procédures récursives dans ce guide,
et c'est une excellente occasion. La particularité d'une procédure récursive (cela
marche aussi avec les fonctions) est de s'appeler elle-même une ou plusieurs fois au
cours de son exécution. Cette possibilité, intensivement employée dans d'autres
langages tels LISP, l'est assez peu en Pascal. Lorsqu'on programme une
fonction/procédure récursive, il faut prévoir ce qui s'appelle une condition
d'arrêt, car sinon les appels imbriqués sont infinis et finissent par saturer la
mémoire. C'est le même principe qu'avec une boucle while ou repeat.
Dans notre cas, la procédure de suppression d'un arbre va s'appeler au plus deux
fois pour supprimer chacun des deux sous-arbres (non vides). La condition d'arrêt
sera trouvée lorsque les deux sous-arbres seront vides (on sera arrivé à une
"feuille"). Le principe est le suivant : pour supprimer un arbre non vide, on
supprime d'abord son sous-arbre gauche s'il n'est pas vide, puis de même avec
son sous-arbre droit. Après ces deux appels, il ne reste plus qu'à supprimer le
noeud racine en libérant la mémoire allouée. Voici ce que cela donne :
procedure DetrArbin(A: TArbin);
begin
// destruction complète d'un arbre binaire
if A <> nil then
begin
// destruction du sous-arbre gauche
if A^.FG <> nil then
DetrArbin(A^.FG);
// destruction du sous-arbre droit
if A^.FD <> nil then
DetrArbin(A^.FD);
// destruction du noeud racine
Dispose(A);
end;
end;Voilà, c'est à peu près tout pour les arbres binaires. Je ne donne pas d'exemple concret de leur utilisation car le mini-projet qui suit va vous permettre de vous exercer un peu par vous-même. C'est un sujet qui pourraît être traité de manière beaucoup plus simple, mais le but est avant tout de vous faire manipuler les structures d'arbre binaire, de pile et de liste.
XV-G. Mini-projet : calculatrice▲
Le texte du mini-projet n'est pas encore terminé. Je le mettrai en ligne dés que possible et j'enverrai un message sur laliste de diffusionpour prévenir de sa disponibilité.